|
|
| |||||||||||||||||||||||||||||||||||||||
|
Funktionen (auch Abbildungen genannt) gehören zu den wichtigsten mathematischen Objekten überhaupt. Nicht nur innerhalb der Mathematik, sondern in in nahezu allen Anwendungen spielen sie eine unverzichtbare Rolle. Diese universelle Anwendbarkeit rührt daher, daß die dahintersteckende Idee eine sehr einfache und schöne ist. Was also ist eine Funktion? Unter einer Funktion kann man sich eine Input-Output-Maschine (Eingabe-Ausgabe-Maschine) vorstellen. Sie nimmt ein Ding als Eingabe entgegen und gibt daraufhin ein Ding aus. Und das macht sie nach einer genauen (eindeutigen) Vorschrift - gleiche Eingaben führen immer zu gleichen Ausgaben. Das ist alles!
"Ding" bedeutet vorläufig für uns "Zahl". Eine Funktion ist also für uns
zunächst eine Maschine, die aus einer Eingabe-Zahl eine Ausgabe-Zahl macht.
Hier haben wir eine solche Maschine:
Geben Sie eine Zahl ein und klicken Sie auf den Button! Geben Sie eine andere Zahl ein und klicken Sie wieder auf den Button! Bevor Sie weiterlesen, wiederholen Sie das öfter und versuchen Sie, herauszufinden, was diese Maschine mit den von Ihnen eingegebenen Zahlen macht! Sie werden sicher nicht lange brauchen, um es herauszufinden: Die Maschine quadriert die Eingabe-Zahl! Es ist eine Quadrier-Maschine. Sie stellt die Idee dar, daß jeder Zahl x ihr Quadrat x2 zugeordnet wird. Ihre Zuordnungsvorschrift heißt schlicht und einfach "quadrieren". Dadurch ist eine Funktion definiert. Wir könnten sie "Quadrier-Funktion" nennen. Die Zuordnung ist eindeutig: Gleiche Eingaben führen immer zu gleichen Ausgaben, wie wir schon oben gesagt haben. Man könnte nun umgekehrt fragen, ob aus der Ausgabe auf die Eingabe rückgeschlossen werden kann. Wenn die Ausgabe die Zahl 4 ist - was war die Eingabe? Wenn Sie jetzt sagen "die Zahl 2", so haben Sie nicht ganz recht - es könnte auch -2 gewesen sein! Der Rückschluß auf die Eingabe ist also nicht zwangsläufig möglich! Die zwei Zahlenfelder in unserer Quadrier-Maschine sind nicht "gleichberechtigt". Wenn wir wissen, was im linken (Eingabe-)Feld steht, wissen wir, was im rechten (Ausgabe-)Feld steht (nämlich das Quadrat der Eingabe), aber aus der Kenntnis der Ausgabe folgt nicht notwendigerweise die Kenntnis der Eingabe. Funktionen arbeiten daher in einer "Richtung":
und diese Richtung ist auch in der obigen Maschine durch einen Pfeil gekennzeichnet.
Nun betrachten wir eine andere Maschine:
Was macht diese Maschine mit Ihren eingegebenen Zahlen? Bevor Sie weiterlesen, versuchen Sie, es herauszufinden!
Haben Sie es geschafft? Die Maschine verdoppelt die Eingabe-Zahl und subtrahiert 1.
Die Zuordnungsvorschrift heißt jetzt "verdoppeln und 1 subtrahieren".
Wir haben es hier mit der "Verdoppeln-und-1-subtrahieren-Funktion" zu tun, und Sie sehen
sicher ein, daß es jetzt besser ist, eine abgekürzte Schreibweise zu verwenden,
um zu beschreiben, was unsere Maschinen tut. Sie stellt einfach die Idee dar,
daß jeder Zahl
x
die Zahl
Wir haben bisher zwei Funktionen betrachtet:
besteht darin, nach dem Namen der Funktion einen Doppelpunkt zu machen und die Zuordnungsvorschrift mit einem Pfeil zu kennzeichnen:
 .
Aus technischen Gründen verwenden wir aber das Symbol ®).
Damit können wir die Quadrier-Maschine - die ja nun schlicht und einfach
f
heißt - ordentlich beschriften: .
Aus technischen Gründen verwenden wir aber das Symbol ®).
Damit können wir die Quadrier-Maschine - die ja nun schlicht und einfach
f
heißt - ordentlich beschriften:
Jetzt ist eindeutig zum Ausdruck gebracht, was sie macht (oder, wie man auch sagt, wie die Funktion wirkt) - sie quadriert. Im Eingabefeld steht eine beliebig vorgegebene Zahl x, im Ausgabefeld deren Quadrat x2. In derselben Weise wird die Wirkung der Funktion g kurz als
Mit Hilfe dieser kleinen zusätzlichen Beschriftung können Sie nun viel besser kontrollieren, welche Ausgaben Sie erwarten: Setzen Sie ihre Eingabe-Zahl x in den Ausdruck Die Schreibweise mit Zuordnungs-Pfeil drückt aus, daß hier von einer beliebigen Eingabe-Zahl ausgegangen wird und gemäß einer gewissen Vorschrift eine Ausgabe erfolgt. Es gibt auch gar keinen zwingenden Grund, die Eingabe-Zahl unbedingt mit dem Buchstaben x zu bezeichnen. So kann die Funktion f anstelle von (1) etwa auch in der Form
Die Schreibweise mit Zuordnungs-Pfeil kann auch angewandt werden, um anzuschreiben, was mit konkreten Eingabe-Zahlen unter der Wirkung einer Funktion geschieht, z.B. im Fall der Funktion f
Neben der Schweibweise mit Zuordnungs-Pfeil ist eine weitere
Notation gebräuchlich, die in der Praxis sogar noch nützlicher
ist.
| |||||||||||||||||||||||||||||||||||||||
Betrachten wir wieder die Funktion
f :
x ®
x2, die die Eingabe-Zahl
quadriert. Klarerweise hängt die Ausgabe von der Eingabe ab.
Sehr oft möchte man dieses Abhängigkeitsverhältnis in der
Schreibweise noch einfacher zum Ausdruck bringen. Dies wird bewerkstelligt, indem die
Wirkungsweise der Funktion in der Form
Die Zeichen Bei dieser Schreibweise gilt allgemein das Schema
Der Vergleich einer Funktion mit einer Maschine ist hier besonders
augenfällig: Zwischen den "von"-Klammern befindet sich, bildlich gesprochen,
das Eingabefeld. Eine beliebige Zahl kann anstelle der Punkte in
Wieder kommt es auf das verwendete Symbol nicht an, und wir können die Funktion f anstelle von (5) genausogut in der Form
Um diese Schreibweise kurz zu illustrieren, stellen wir
die Frage, was Unsere Funktion g kann ganz analog in der Form
Die Abhängigkeit einer Größe von einer anderen, die durch diese Schreibweise
ausgedrückt wird, ist ein wichtiger Aspekt des Funktionsbegriffs. Ist etwa der Wert einer
Größe y davon abhängig, welchen Wert
eine andere Größe x hat
(einige praktische Beispiele folgen unten), so
wird die abhängige Größe y oft einfach als y(x) angeschrieben, d.h. das Symbol
y gleichzeitig als Name für eine Größe (Variable)
und für eine Funktion verwendet. (Die abhängige Größe y
entspricht dem "Output", die unabhängige Größe x
dem "Input" unserer Funktionsmaschinen).
Mit Hilfe des nebenstehenden Applets können derartige Abhängigkeiten
- auf nicht ganz konventionelle Weise -
dynamisch visualisiert werden. | Funktionale Abhängigkeiten verstehen | ||||||||||||||||||||||||||||||||||||||
|
Eine Funktion ist natürlich keine "Maschine" im mechanischen Sinn, und auch kein Computerprogramm - sie besteht lediglich aus einer eindeutigen Zuordnungsvorschrift. Weiters kann es solche Vorschriften auch für andere mathematische Objekte als Zahlen geben. Ganz allgemein benötigt man für eine Funktion zwei Mengen (die wir hier A und B nennen). Definition: Eine Funktion (auch Abbildung genannt) f "von der Menge A in die Menge B" ist eine Vorschrift, die jedem Element von A in eindeutiger Weise ein Element der Menge B zuordnet. Um auszudrücken, daß f eine solche Funktion ist, wird
| |||||||||||||||||||||||||||||||||||||||
|
In unseren bisherigen Beispielen war
A = B =
R, der Menge der reellen Zahlen.
In den meisten Fällen von Funktionen, denen wir begegnen werden, wird
A (die Menge, aus der die Eingabe-Werte
beliebig gewählt werden können) entweder
R oder eine Teilmenge von
R sein. Die Ausgabe-Werte werden meistens reelle Zahlen
sein, d.h.
B = R.
Man spricht dann von reellen Funktionen. Nun wissen Sie im Prinzip, was eine mathematische Funktion ist. Wir haben Anwendungen und Motivationen ausgespart und statt dessen die Metapher der Input-Output-Maschine verwendet, um Ihnen einen möglichst raschen Zugang zu diesem wichtigen Begriff zu ermöglichen. Sie werden in der Folge (in diesem Kapitel wie in zahlreichen anderen) die verschiedensten Funktionen kennenlernen. Sie werden erfahren, wofür man sie verwendet und wie gewinnbringend mit ihnen hantiert werden kann. |  reelle Zahlen | ||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||
|
Immer dann, wenn der Wert einer Größe vom Wert einer anderen Größe abhängt, liegt eine Funktion vor. Da die Natur und unser Leben voll von solchen Abhängigkeiten sind, kann eine unermesslich große Anzahl von Vorgängen und Zusammenhängen in der mathematischen Sprache der Funktionen beschrieben, modelliert und verstanden werden - manchmal sehr genau, in Form ausgefeilter Theorien, manchmal nur in grober Näherung. Betrachten Sie etwa ein Thermometer, das an irgendeinem Ort hängt. Die von ihm angezeigte Temperatur wird nicht immer dieselbe sein, sondern sich mit der Zeit ändern, z.B. tages- oder jahreszeitlichen Schwankungen unterworfen sein. Mit anderen Worten, die Temperatur hängt vom Zeitpunkt ab, an dem sie gemessen wird. Dies stellt eine Input-Output-Maschine, d.h. eine Funktion dar: Zu jedem gegebenen Zeitpunkt t (Eingabe) wird eine bestimmte Temperatur T (Ausgabe) angezeigt. Man sagt, die Temperatur "ist eine Funktion der Zeit". Wie bereits oben bemerkt, ist es üblich, das Symbol für den Ausgabe-Wert ( hier T ) als Namen der Funktion zu verwenden. Jedem Zeitpunkt t ist dann eine Temperatur T(t) zugeordnet. Jedes konkrete Thermometer, das Sie sich aussuchen, definiert eine solche Funktion. Ob sich die Temperatur aufgrund einer Theorie berechnen läßt oder ob sie abgelesen werden muß, ist dabei unerheblich - in jedem Fall handelt es sich um eine Funktion, denn zu jedem Zeitpunkt t wird eine bestimmte Temperatur T angezeigt.
Weitere Beispiele für derartige Abhängigkeiten können Sie
mit Hilfe des nebenstehenden Buttons aufrufen. | |||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||
|
Wir haben im ersten Abschnitt dieses Kapitels den Funktionsbegriff anhand der Idee einer Input-Output-Maschine entwickelt. Hier wollen wir die in der Mathematik übliche Sprechweise über einige Dinge festhalten. Da Funktionen wichtige Objekte sind, wurde im Laufe der letzten Jahrhunderte viel über sie gesprochen (und geschrieben). Als Folge haben sich mehrere Sprechweisen über ein und dieselbe Sache herausgebildet. Die meisten Worte stammen direkt aus der Alltagssprache.
Folgende Begriffe, die in den mathematischen Wortschatz über Funktionen gehören,
werden wir erwähnen:
Wenn diese Materie für Sie völlig neu ist, ...
... werden Sie sich vielleicht erschlagen fühlen, wenn Sie die folgende Vokabelsammlung lesen.
Das haben Vokabelsammlungen leider so an sich.
Wenn Sie sich schwer damit tun, versuchen
Sie zumindest, sie zu
überfliegen.
An viele der hier vorgestellten Redewendungen
werden Sie sich gewöhnen, wenn Sie sie selbst eine Zeitlang benützen.
Eine Funktion (oder Abbildung)
Schreibweisen für die Definition von Funktionen anhand eines Beispiels
(die Funktion "quadrieren", mit
Das Symbol x
steht für ein
beliebiges Element der Menge A
(Eingabe-Wert), das der Wirkung der Funktion unterworfen werden kann - man nennt es daher
Variable (altmodischer Ausdruck: Veränderliche),
da es für eine "variable" Größe steht
(oder unabhängige Variable, da es beliebig - von nichts abhängig -
vorgegeben werden kann).
Eine andere Bezeichnung dafür ist Argument.
Ein konkreter Wert der unabhängigen Variablen (des Arguments)
wird auch als Stelle oder auch als
x-Wert bezeichnet.
Das einem konkreten Element
Zur Illustration dieses Sprachgebrauchs: Wo hat die durch
Die Funktion wirkt auf die Elemente von A, sie wird auf diese angewandt (angewendet). Elemente von A werden in die Funktion eingesetzt. Jedes Element von A wird auf ein Element von B abgebildet.
Manchmal wird auch ein eigenes Symbol für die möglichen Funktionswerte verwendet,
z.B. der Buchstabe y.
Das ist dann so gemeint, daß zu jedem
Beispiel: Ein Fahrzeug fährt von Bregenz nach Wien, x steht für die seit Reisebeginn verstrichene Zeit, und y ist die zurückgelegte Strecke. Daher ist y eine Funktion von x. Die Größe y wird daher auch abhängige Variable (oder abhängige Größe) genannt.
Der funktionale Zusammenhang (die Zuordnungsvorschrift), der festlegt,
welcher y-Wert
aus einem gegebenen
x-Wert entsteht ( also die
zugrundeliegende Funktion
f )
wird dann als
Beispiel: Die durch
| |||||||||||||||||||||||||||||||||||||||
|
Die Bedeutung der unabhängigen Variablen ähnelt ein bißchen der
Bedeutung der Variablen in Termen. Das für sie verwendete Symbol
(z.B. der Buchstabe x) ist ein
Platzhalter, für den jeder konkrete Wert - d.h. jedes
Element der Menge A -
eingesetzt werden kann. Wird z.B. in die Funktionsdefinition
|  Variable und Terme | ||||||||||||||||||||||||||||||||||||||
|
Die meisten in der Schulmathematik auftretenden Funktionen wirken auf reelle Zahlen,
d.h. für sie ist A gleich der (oder
eine Teilmenge der) Menge R
der reellen Zahlen. Diese Funktionen heißen Funktionen in einer Variablen.
Sie drücken eine Situation aus, in der eine Größe (z.B. der Treibstoff-Verbrauch
während einer Reise)
von einer anderen Größe abhängt (z.B. von der Länge der Reise-Route).
Jede einigermaßen
realistische Größe hängt aber in Wahrzeit von zahlreichen
Größen
ab (in unserem Beispiel z.B. auch von der Geschwindigkeit, der Steigung,...).
Solche Situationen führen auf Funktionen in mehreren Variablen,
für die die Menge A nicht aus reellen Zahlen,
sondern aus Kombinationen von reellen Zahlen (z.B. Zahlenpaaren oder Zahlentripeln)
besteht. |  Funktionen in mehreren Variablen | ||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||
|
Wie haben oben besprochen, in welchen Schreibweisen Funktionen charakterisiert werden können (Schreibweise mit Zuordnungs-Pfeil, Schreibweise mit "von"-Klammer). Das waren eher formale Betrachtungen, und so wollen wir uns der Frage zuwenden, wie die Wirkung einer Funktion mathematisch beschrieben wird.
Wir haben bisher zur Illustration zwei Funktionen kennengelernt:
Eine Funktion namens f, deren Wirkung durch
|  Terme | ||||||||||||||||||||||||||||||||||||||
Überzeugen Sie sich durch Probieren, daß diese Maschine tatsächlich nichts anderes macht, als jeden Eingabe-Wert x in den Term (Setzen Sie z.B. Auf analoge Weise definiert jeder Term (der von einer einzigen Variablen abhängt) eine Funktion! Es gibt also unermesslich viele Funktionen! Die Beschreibung der Wirkungsweise eine Funktion durch einen Term - wie es in allen Formeln (1) bis (7) und (9) geschehen ist - heißt Termdarstellung. Ein Term, der eine Funktion definiert, wird auch Funktionsausdruck genannt.
Der Rest dieses Abschnitts
kann von
''EinsteigerInnen'' ausgelassen werden. | |||||||||||||||||||||||||||||||||||||||
Achtung: Nicht jeder Term definiert eine Funktion
Die bisher betrachteten Funktionen waren durch einen Term beschrieben, der lediglich
die Grundrechnungsarten (und ihre Abkömmlinge wie Wurzelziehen)
auf die Variable x
anwendet. Es gibt allerdings Funktionen, für die es nicht leicht fällt
(oder ganz unmöglich ist), einen solchen Term
hinzuschreiben, die aber dennoch eine sinnvolle und leicht verständliche
Wirkung haben.
Vier Beispiele dafür, | |||||||||||||||||||||||||||||||||||||||
Durch diese Beispiele wird illustriert: Was bei der Definition von Funktionen zählt, ist
die eindeutige Zuordnungvorschrift. Ob diese durch einen einfachen Term realisierbar ist,
Fallunterscheidungen erfordert oder am besten in Worten mitgeteilt werden kann,
ist nicht so wichtig. Das ist der Hauptunterschied
zwischen einem Term und einer Funktion! | |||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||
|
Wenn wir irgendeine Funktion - also eine Zuordnungsvorschrift, wie jeder Zahl (wir nennen sie x) wiederum eine Zahl (der Funktionswert) zugeordnet wird - gegeben haben, ist es manchmal notwendig, sich einen groben Überblick zu verschaffen, wie sie wirkt. So kann zum Beispiel in regendeinem Zusammenhang relevant sein, für welche Werte von x der Funktionswert Null ist, oder welches Vorzeichen der Funktionswert hat, wenn x eine sehr groß,e Zahl ist. Eine Möglichkeit, sich einen ersten Überblick zu verschaffen, sind sogenannte Wertetabellen. Damit ist gemeint, in Form einer Tabelle mehrere x-Werten den zugehörigen Funktionswerten gegenüberzustellen, also einige Beispiele für die Wirkung der Funktion anzuschreiben.
Wir wollen das am Fall der Funktion g, die durch
Sie erhalten 17 verschiedene x-Werte, deren Abstand die von Ihnen gewählte Schrittweite ist, zusammen mit den jeweiligen Funktionswerten. Neben jeder Zahl x in der linken Spalte steht der Funktionswert Sie können eine neue Schrittweite eingeben und den Button erneut drücken. Probieren Sie es mit den Werten 100,10, 0.5, 0.1 und 0.01 ! Verwenden Sie diese dynamische Tabelle, um folgende Fragen zu beantworten:
| |||||||||||||||||||||||||||||||||||||||
|
So lassen sich für jede Funktion (die die Rechenkünste von Menschen und Computern nicht übersteigt) Wertetabellen anschreiben. Da jede Tabelle nur endlich viele Zahlen umfassen kann, müssen die dargestellten Werte (je nach Fragestellung) sinnvoll gewählt werden.
Aufgabe: Schreiben Sie auf einem Blatt Papier eine kleine Wertetabelle
für die durch
| |||||||||||||||||||||||||||||||||||||||
|
Wertetabellen ermöglichen einen groben Überblick über die Eigenschaften einer Funktion. Sie waren in der Zeit vor dem Einsatz des Computers besonders dann hilfreich, wenn numerisch sehr genaue Werte einer Funktion erforderlich waren. Dicke Tabellenwerke (z.B. die sogenannten "Logarithmentafeln") waren bis ins 20. Jahrhundert hinein die ständigen Begleiter der MathematikerInnen. |  Logarithmus | ||||||||||||||||||||||||||||||||||||||
|
Allerdings sind Zahlenkolonnen unanschaulich, und sehr viel Information springt aus einer Wertetabelle nicht gerade ins Auge. Es gibt eine viel bessere Methode, wichtige Eigenschaften von Funktionen mit einem Blick zu überschauen, nämlich eine graphische. Dieser wenden wir uns nun zu. | |||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||
|
Graphische Darstellung von Wertetabellen Jede Zeile in einer Wertetabelle (siehe oben) besteht aus einem Paar von Zahlen: ein Wert für die unabhängige Variable (den wir wieder kurz x-Wert nennen), zusammen mit dem zugeordneten Funktionswert. Jedes solche Zahlenpaar kann graphisch als Punkt in einer Ebene dargestellt werden. | |||||||||||||||||||||||||||||||||||||||
|
Dazu erinnern wir uns, daß die Ebene (Zeichenebene)
mit zwei zueinander orthogonalen Achsen ausgestattet werden kann.
Die Lage jedes Punktes ist dann durch zwei Zahlen (seinen Koordinaten) beschrieben.
Nennen wir sie, wie üblich,
x-Achse ("horizontal") und
y-Achse ("vertikal"), so ist die Lage jedes
Punktes durch ein Paar
Ein in der Wertetabelle einer Funktion f auftretendes Zahlenpaar ist immer von der Form
Sehen wir uns das anhand eines konkreten Beispiels an!
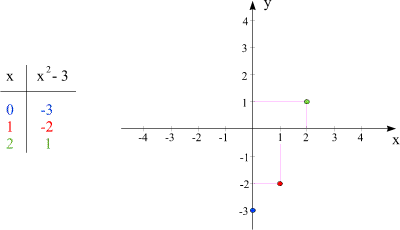
Überprüfen Sie (durch Rechnung) die drei Funktionswerte (-3, -2 und 1) in der Wertetabelle! Überprüfen Sie die Positionen der drei Punkte anhand der Zahlen in der Wertetabelle! Die Wertetabelle enthält genausoviel Information wie die Position der drei Punkte: Haben Sie die Wertetabelle gegeben, so können Sie die drei Punkte einzeichnen. Falls Sie andererseits nur den rechten Teil der Graphik kennen, so können Sie durch Ablesen der Koordinaten der drei Punkte die Wertetabelle rekonstruieren. Das Koordinatensystem mit den drei Punkten ist nichts anderes eine graphische Darstellung der Wertetabelle.
Nun betrachten wir dieselbe Funktion, aber eine umfangreichere Wertetabelle:
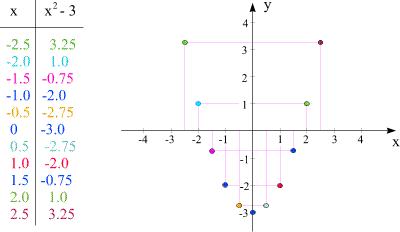
Die Zeilen (Zahlenpaare) der Wertetabelle sind in denselben Farben wie die entsprechenden Punkte im x-y-Koordinatensystem eingezeichnet. Überprüfen Sie die Positionen der elf Punkte anhand der Zahlen in der Wertetabelle!
Werden die Zahlen entlang der Achsen und die Hilfslinien weggelassen, so sieht die
Graphik so aus:
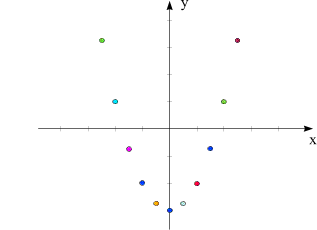
Wir sehen: besitzt die Wertetabelle einigermaßen viele Entragungen, so "nimmt die Funktion Gestalt an". In der Mathematik wird oft mit den so entstehenden "Gestalten" hantiert. Fassen wir zusammen, was uns dieses Beispiel sagt:
Salopp wird die Vorschrift, einen Funktionsgraphen zu zeichnen
so ausgedrückt, daß der zu einem Punkt auf der
x-Achse gehörende Funktionswert
"nach oben" (oder, wenn er negativ ist, "nach unten") aufgetragen wird.
Ist umgekehrt ein Punkt mit Koordinaten
Wertetabellen haben den Nachteil, daß sie nur ausgewählte Beispiele für x-Werte beinhalten. Eine Wertetabelle beinhaltet immer weniger Information als die Funktion (die Zuordnungsvorschrift) selbst. Um dieser Einschränkung zu entkommen, definieren wir nun ein geometrisches Objekt, das alle möglichen x-Werte berücksichtigt:
Definition: Der Graph einer Funktion
f :
R ®
R
ist die Menge aller Paare
In der Mengenschreibweise ist er |  Koordinaten | ||||||||||||||||||||||||||||||||||||||
Da die Zeichenebene mit der Menge aller Zahlenpaare identifiziert wird, kann der Graph einer Funktion als Teilmenge der Zeichenebene betrachtet werden. Für die meisten uns interessierenden Funktionen ist er eine Kurve (eine Gerade oder eine gebogene Linie).
Das sehen wir uns wieder an dem Beispiel der durch
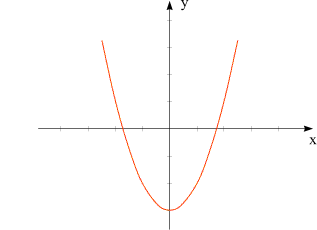
|  Mengen und ihre Beschreibung | ||||||||||||||||||||||||||||||||||||||
|
Vergleichen sie ihn mit der oben wiedergegebenen
graphischen Darstellung einer Wertetabelle aus elf Zeilen!
Jede Zeile der Wertetabelle entspricht einem Punkt auf dieser Kurve.
(Letztere heißt übrigens
Parabel - wie werden ihr noch öfter begegnen; siehe auch
die Besprechung der Graphen einfacher Polynomfunktionen (unten).
Am Bildschirm (oder in jeder realen Zeichnung) ist ein Funktionsgraph
nichts anderes als die graphische Darstellung einer umfangreichen Wertetabelle.
Stellen Sie sich vor, eine Wertetabelle unserer Funktion
f mit zweihundert
x-Werten
(zwischen
Es gibt eine zu (12) alternative Schreibweise, die sehr wichtig ist. Für die x- und y-Koordinaten jedes Punktes eines Funktionsgraphen gilt
|  Parabel (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||
|
erfüllt ist. Diese wird als Funktionsgleichung bezeichnet. Sie ist
eine Gleichung in den zwei Variablen
x und
y. Jeder Punkt mit Koordinaten
Um die Wirkung einer Funktion zu beschreiben, wird anstelle einer Angabe wie
|  Gleichungen und Lösungsmenge | ||||||||||||||||||||||||||||||||||||||
|
Die Definition (13) ist Spezialfall einer allgemeineren Beschreibung von Kurven in der Zeichenebene. Kurven und (Graphen von) Funktionen hängen miteinander zusammen, sind aber nicht ganz dasselbe.
Frage: Ist jede Kurve in der Zeichenebene der Graph einer Funktion?
|  Kurven (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||
|
Zwei Beispiele, die das illustrieren, können Sie mit Hilfe des nebenstehenden Buttons aufrufen. Geometrisch bedeutet das: Eine Kurve, die eine zur y-Achse parallele Gerade in mehreren Punkten schneidet, ist nicht Graph einer Funktion. Definitionsbereich beachten! Bisher haben wir nur über Graphen von Funktionen
Beispiel: Die Funktion
| |||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||
|
In diesem Abschnitt wollen wir einige konkrete Funktionsgraphen besprechen. Sie treten in abgewandelter Form auch oft bei allgemeineren Funktionen auf und bilden wichtige "Bausteine" unseres Verständnisses von Funktionen. Eine Potenzfunktion ist eine Funktion der Form
| |||||||||||||||||||||||||||||||||||||||
|
Dabei bedeuten negative Exponenten das zusätzliche Bilden des Kehrwerts:
x-1
bedeutet einfach
1/x,
x-2
bedeutet
1/x2, usw.
Wir werden den Grund für diese Schreibweise in einem späteren Kapitel
besprechen.
Für n = 1 ergibt sich Sie können die Graphen dieser Funktionen (und noch zwei weiterer, damit verwandter) betrachten, indem Sie auf den Button Folgender Button ruft eine kurze Besprechung dieser Funktionen auf. (Manche der Graphen sind Kurven, die in den verschiedensten Zusammenhängen auftreten und eigene Namen erhalten haben, insbesondere: erste und zweite Mediane, Parabel, Hyperbel). |  negative Exponenten | ||||||||||||||||||||||||||||||||||||||
|
Anhand dieser zehn Beispiele läßt das Verständnis dafür schärfen,
wie sich die Zuordnungs-Vorschrift einer Funktion in ihrem Graphen wiederspiegelt.
Mit Hilfe des nebenstehenden
Buttons können Sie einige weiterführende
Übungsfragen über die ersten sechs dieser Funktionen
(jene mit positivem Exponenten) aufrufen. | |||||||||||||||||||||||||||||||||||||||
|
Die letzten vier Funktionen weisen negative Exponenten auf. Wir können sie als
|  Asymptoten | ||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||
|
Dieser Abschnitt macht Sie mit einigen Begriffen, Zusammenhängen und Methoden bekannt, die bei der Anwendung und Analyse von Funktionen hilfreich sind. Sie kommen in vielen Teilgebieten der modernen Mathematik zum Einsatz. Eine Funktion f ordnet, ganz allgemein gesprochen, jedem Element einer Menge A ein (eindeutig bestimmtes) Element einer Menge B zu. Wird eine Funktion definiert, so müssen genau genommen beide Mengen A, B und die Zuordnungsvorschrift f angegeben werden. Bei der Wahl der Menge B besteht einige Freiheit. Es muß nur sichergestellt werden, daß alle Funktionswerte in B liegen - mit anderen Worten, B muß "groß genug" sein. In den von uns am häufigsten betrachteten Fällen bestehen A und B aus reellen Zahlen, sind also entweder R oder Teilmengen von R. Man kann dann immer
Wie bereits oben erwähnt, heißt die Menge A
der Definitionsbereich der Funktion f.
Die Menge aller Elemente von B, die von der
Funktion "getroffen werden", d.h. die als Funktionswert von zumindest einem
Der Wertebereich kann als "Menge aller am Graphen auftretenden
y-Werte" ermittelt werden.
Ist die Funktion an der Stelle Seien A und B Teilmengen von R und Eine Nullstelle der Funktion f ist ein
Nullstellen können leicht erkannt werden, wenn der Graph der Funktion einmal gezeichnet ist:
Jedem Paar Nun kommt etwas Wichtiges: Ist
| |||||||||||||||||||||||||||||||||||||||
|
im Allgemeinen für die meisten
Nullstellen werden berechnet durch das Lösung einer Gleichung! (Als Beispiele dafür werden wir weiter unten einfache Polynomfunktionen besprechen).
Gehen wir umgekehrt von einer Gleichung der Form
Das führt auf eine allgemeine Methode zum näherungsweisen Lösen von Gleichungen
der Form
|  Gleichungen | ||||||||||||||||||||||||||||||||||||||
Daneben stehen noch andere Methoden zur Verfügung, Lösungen von Gleichungen nägerungsweise zu finden.
Wir werden in späteren Kapiteln einige solcher numerischen Lösungsmethoden
kennen lernen:
|  Bisektionsmethode (in Vorbereitung) Newton-Verfahren * Nullstellen von Polynomen | ||||||||||||||||||||||||||||||||||||||
|
Achtung: Falls der Term
Diese Methode besitzt eine Verallgemeinerung: |  Definitionsmenge einer Gleichung | ||||||||||||||||||||||||||||||||||||||
|
An dieser Stelle ist es sinnvoll, das Applet Funktion und Funktionsgraph
durch nebenstehenden Link aufzurufen. Es hilft Ihnen, sich die Dinge, von denen hier die Rede
ist, besser vorzustellen und mit der mathematischen Symbolsprache zu verbinden.
Die Arbeit, den Graphen einer gegebenen Funktion zu zeichnen, kann heute der
Computer übernehmen. Er hilft auch dabei, Nullstellen (oder Schnittpunkte
zweier Graphen) mit hoher Genauigkeit zu ermitteln..
Wir werden unten über den mathe online Funktions-Plotter sprechen,
der Sie mit Hilfe seiner Zoom-Funktion in die Lage versetzt, die meisten Gleichungen, mit denen Sie konfrontiert werden,
näherungsweise
zu lösen.
Ist die Funktion f an der Stelle x positiv (d.h.
Funktionen können in manchen Intervallen positiv, in anderen
Intervallen negativ sein. Die Grenzen dieser Intervalle
bilden die Nullstellen.
Eine Funktion f heißt
| Funktion und Funktionsgraph | ||||||||||||||||||||||||||||||||||||||
|
Diese vier Monotonie-Typen können leicht am Graphen erkannt werden als "ansteigen-oder-gleichbleiben", "ansteigen", "abfallen-oder-gleichbleiben" und "abfallen", während die x-Koordinate nach "rechts" wandert. Eine Funktion kann natürlich in verschiedenen Intervallen verschiedene Monotonie-Eigenschaften besitzen. (Diese werden dann manchmal als Monotonie-Intervalle oder Monotonie-Bereiche bezeichnet). Monotone Funktionen dienen der Modellierung von Zu- und Abnahmeprozessen (Wachstum und Zerfall), wie anhand der Exponentialfunktionen in einem späteren Kapitel ausführlich diskutiert werden wird. In einem darauffolgenden Kapitel werden sie bei der Analyse von dynamischen Systemen auftreten. Der Rest dieses Abschnitts kann von ''EinsteigerInnen'' ausgelassen werden. Sei |  Intervall  Wachstum  dynamische Systeme (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||
|  mehr über die inverse Funktion | ||||||||||||||||||||||||||||||||||||||
|
Diese Begriffe dienen - neben anderen Zwecken - dazu, Mengen miteinander zu
vergleichen. Sie gewähren tiefe Einblicke in die Natur von Mengen, die unendlich
viele Elemente haben. Existiert etwa zwischen zwei Mengen eine bijektive Funktion,
so sind sie "gleich groß" (genauer: gleichmächtig
- ein Begriff, der uns schon früher begegnet ist).
In gewissem Sinn kann man sie dann miteinander identifizieren.
(Bei der Besprechung der Grundlagen der Mengenlehre haben wir solche
Mengen auch als zueinander "isomorph" bezeichnet.
Eine bijektive Funktion wird in
diesem Zusammenhang auch als Isomorphismus
bezeichnet). |  gleichmächtig und isomorph | ||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||
|
Funktionen, die durch ein Polynom (eine "ganzrationale Funktion") nullter, erster oder zweiter Ordnung definiert werden, werden häufig benötigt. Sie können eine systematische Zusammenstellung der dabei auftretenden Typen aufrufen, indem Sie auf den Button. |  Polynome | ||||||||||||||||||||||||||||||||||||||
|
klicken. Die Koeffizienten des jeweiligen Polynoms sind mit
d, k,
a, b und
c bezeichnet. Sie können beliebig vorgegeben werden.
Die Graphen dieser Funktionen sind entweder Geraden oder Parabeln.
Ihre Lage hängt von den jeweiligen
Koeffizienten ab.
Konstante Funktionen und Funktionen erster Ordnung ... |  Koeffizienten | ||||||||||||||||||||||||||||||||||||||
Achtung - kleines Bezeichnungs-Wirrwarr: | |||||||||||||||||||||||||||||||||||||||
| Der Koeffizient d ist der zum x-Wert 0 gehörende Funktionswert. Er wird kurz Abschnitt auf der y-Achse genannt und bezeichnet die y-Koordinate des Schnittpunkts zwischen der Geraden und der y-Achse. Der Koeffizient k ist ein Maß für die "Steilheit" der Geraden. Er heißt Anstieg oder Steigung. Die Beschreibung der Lage von Geraden in einem Koordinatensysten und die Bedeutung der beiden Koeffizienten k und d wird in einem anderen Kapitel ausführlicher besprochen. |  Beschreibung von Geraden (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||
|
Es gibt mehrere Methoden, die Lage des Graphen einer gegebenen Funktion erster Ordnung zu ermitteln. Die einfachste ist, zwei Punkte zu finden, die auf ihm liegen (also eine Wertetabelle mit zwei Zeilen zu erstellen) und in ein Koordinatensystem einzuzeichnen. Da der Graph eine Gerade ist, kann diese dann sofort mit Hilfe eines Lineals gezogen werden.
Ist |  lineare Gleichungen | ||||||||||||||||||||||||||||||||||||||
|
Ist umgekehrt eine (nicht zur y-Achse parallele) Gerade gegeben, so ist sie der Graph einer konstanten Funktion (falls sie parallel zur x-Achse ist) oder einer Funktion erster Ordnung (sonst). Funktionen zweiter Ordnung (quadratische Funktionen) ...
| |||||||||||||||||||||||||||||||||||||||
|
Parabeln sind altehrwürdige Kurven. Ihre geometrischen Eigenschaften werden in einem anderen Kapitel genauer besprochen.
Beispiele für Funktionen zweiter Ordnung haben wir in diesem Kapitel bereits
kennengelernt: Die "Quadrierfunktion"
Die Lage des Graphen einer Funktion zweiter Ordnung wird durch eine Analyse des sie
definierenden quadratischen Terms ermittelt. Je nach dem Vorzeichen von
a ist die Parabel nach ober oder nach unten offen.
Der Absolutbetrag von a entscheiden über
die Form der Parabel: Ist |  Parabel (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||
Quadratische Ausdrücke sind uns bereits in einem früheren Kapitel früher begegnet.
Einige ihrer Eigenschaften bekommen nun eine anschauliche geometrische Bedeutung:
|  Applet Quadratische Gleichungen 2 | ||||||||||||||||||||||||||||||||||||||
|
Auf diese Weise verhilft uns der Begriff der Funktion zu einem tieferen Verständnis quadratischer Ausrdücke und quadratischer Gleichungen.
Beispiel: Die Nullstellen der oben besprochenen Funktion
Der Spieß kann natürlich umgedreht werden: Ist die Gleichung
|  quadratische Gleichungen | ||||||||||||||||||||||||||||||||||||||
| Die Position der Parabel (insbesondere ihres "untersten" bzw. "obersten" Punktes, des sogenannten Scheitels) kann rechnerisch durch eine Methode ermittelt werden, die wir bereits früher im Zusammenhang mit quadratischen Gleichungen kennengelernt haben: das Ergänzen auf ein vollständiges Quadrat (oder, was auf dasselbe hinausläuft, durch eine Anwendung des Satzes von Vieta). Dies wird in einem anderen Kapitel genauer besprochen. |  Beschreibung von Parabeln (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||
|
Mit Hilfe der zwei nebenstehenden Puzzle-Applets können Sie Ihre Fertigkeit, Funktionsausdrücke und Graphen einander zuzuordnen, üben. Dabei geht es hauptsächlich um Funktionen erster und zweiter Ordnung. Erschrecken Sie nicht, wenn auch eine Funktion dritter Ordnung dabei vorkommt. Erinnern Sie sich an die in diesem Kapitel dargestellten Zusammenhänge zwischen Funktionen und Graphen, um die Aufgaben zu lösen. | Funktionen erkennen 1 und Graphen erkennen 1 | ||||||||||||||||||||||||||||||||||||||
|
Der Rest dieses Abschnitts kann von ''EinsteigerInnen'' ausgelassen werden. Funktionen dritter Ordnung ... ... werden durch Polynome dritter Ordnung dargestellt, d.h. sie sind von der Form
|  Nullstellen von Polynomen | ||||||||||||||||||||||||||||||||||||||
In diesem Kapitel haben wir viel über die Zusammenhänge zwischen
| Polynom höchstens dritter Ordnung | ||||||||||||||||||||||||||||||||||||||
|
Neben graphischen gibt es auch weitere (numerische) Methoden zum Auffinden von Nullstellen, d.h. zum Lösen von Gleichungen - wir sind oben kurz darauf eingegangen. Ein auf dem Computer-Algebra-System Mathematica beruhendes Werkzeug, das polynomische Gleichungen numerisch (und bei niedriger Ordnung auch exakt) lösen kann, ist | |||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||
|
Dieser Abschnitt kann von ''EinsteigerInnen'' ausgelassen werden.
Die Graphen mancher Funktionen haben Ecken. Dies kann insbesondere dann
auftreten, wenn die Funktion durch Fallunterscheidungen (siehe oben) definiert
ist oder die Betragsfunktion (siehe oben) enthält.
Der nebenstehende Button ruft zwei Beispiele dafür auf. Denken Sie bitte nach,
warum die beiden Graphen eine solche Form haben! | |||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||
|
mathe online bietet Ihnen als bequeme Möglichkeit, die Graphen von Funktionen im Detail zu studieren, den Sie werden dieses Werkzeug, ein Java-Applet, oft verwenden können. (Sie können es auch vom Kapitel Funktionen 1 der Galerie und von unserer Ressourcensammlung Mathe-Links und Online-Werkzeuge - Kategorie Online-Werkzeuge > Funktionen und graphische Darstellungen - aus aufrufen). Weitere Programme zum Plotten von Funktionsgraphen finden Sie in den meisten mathematischen Softwarepaketen. Einige davon sind auch online über das Web zugänglich. Wir weisen insbesondere auf das im Rahmen des MathServ Project an der Vanderbilt University zur Verfügung gestellte Werkzeug
Ein weiteres Werkzeug zur Analyse von Funktionsgraphen ist der in Form eines Java-Applets
an der Universität Bayreuth entwickelte
grafische Taschenrechner.
In diesem Kapitel haben wir die Graphen einiger konkreter Funktionen kennengelernt. Wir werden uns später mit weiteren Funktionsgraphen beschäftigen. |  Funktionen 2 | ||||||||||||||||||||||||||||||||||||||
|
|
||
|
|
|
Zum Seitenanfang Zum Lexikon Zur Galerie Zum Kapitel Funktionen 1 der Galerie Zum Inhaltsverzeichnis der Mathematischen Hintergründe Zu den interaktiven Tests Zu den Mathe-Links und Online-Werkzeugen Zur Welcome Page |