|  |
|
| |
|
|
| |||||||||||||||||||||||||||||||||||||||||||
In diesem Kapitel spielen Potenzen, deren Exponenten beliebige reelle Zahlen sein dürfen, eine wichtige Rolle. Daher wollen wir zunächst besprechen, was wir darunter verstehen. Eine Potenz (oder ein Potenzausdruck) ist ein Term der Form ax. Dabei heißt a die Basis und x der Exponent (die Hochzahl). Der Grund dafür, dass wir den Buchstaben x für den Exponenten verwenden, liegt darin, dass wir in diesem Kapitel daran interessiert sind, wie eine Potenz von ihrem Exponenten abhängt. Wir haben bereits früher ausführlich erörtert, wie eine Potenz mit positiver Basis (a > 0) und rationalem Exponenten x definiert ist, und wir erinnern uns an die Rechenregel (Identität) |  Potenzen mit rationalen Exponenten | ||||||||||||||||||||||||||||||||||||||||||
die für alle rationalen Zahlen x, y gilt. Sie hat sich als wertvoller Wegweiser erwiesen und wird auch weiterhin eine zentrale Rolle spielen. Das Bedürfnis nach mathematischer Allgemeinheit legt nun die Frage nahe, ob Potenzen nicht auch für beliebige reelle Exponenten (also auch für irrationale Exponenten, die nicht als Quotient zweier ganzer Zahlen geschrieben werden können, wie Ö2 oder p) definiert werden kann. Kann etwa der Potenz 2p ein Sinn gegeben werden? Wir wollen nun kurz darlegen, dass das tatsächlich möglich ist. Wir benutzen dabei die Tatsache, dass jede irrationale Zahl beliebig genau durch rationale Zahlen angenähert werden kann. Falls es sich beim Exponenten etwa um die Zahl p handelt, betrachten wir die Zahlenfolge und geben in jedem Schritt die nächste Ziffer in der Dezimaldarstellung von p dazu. Diese Zahlen kommen p immer näher (genauer gesagt: sie kommen beliebig nahe an p heran), und sie alle sind rational (so ist etwa 3.14 = 314/100 ein Quotient zweier ganzer Zahlen), daher als Exponenten einer Potenz zulässig. Wir betrachten nun die Potenzen, die wir mit diesen Zahlen bilden können: Um anhand eines Beispiels zu verdeutlichen, wie sich diese Zahlen verhalten, setzen wir a = 2 und sehen uns die Dezimaldarstellungen der ersten sechs Potenzen an:
| |||||||||||||||||||||||||||||||||||||||||||
|
Wir erkennen, dass sich die Zahlen der rechten Spalte immer weniger ändern. Sie streben einer bestimmten reellen Zahl zu, und diese Zahl bezeichnen wir als 2p. Ihre Dezimaldarstellung beginnt mit 8.824977827... In der Fachsprache wird sie als "Grenzwert" der Zahlenfolge, die in der rechten Spalte steht, bezeichnet. Dieselbe Methode kann auch für andere (positive) Basen a und für andere (irrationale) Exponenten x angewandt werden. Da die Rechenregel (1) für rationale Exponenten gilt, durch die wir irrationale Exponenten beliebig gut annähern, dürfen wir annehmen, dass sie auch für letztere gilt. |  Grenzwert (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||||||
|
Wir haben bei dieser Argumentation nicht die allergrößte mathematische Strenge walten lassen,
wollen uns aber dennoch hier mit ihr zufrieden geben.
Einige Bemerkungen darüber, was hinter diesem Verfahren steckt,
können Sie mit Hilfe des nebenstehenden Buttons aufrufen.
Wenn Ihnen unsere Konstruktion ein bisschen umständlich erscheint, so können wir sie beruhigen:
Ihr Zweck liegt nicht in praktischen Berechnungen
- diese werden wir nach wie vor an elektronische Rechner
delegieren.
Der Sinn unserer Argumentation war lediglich, uns (theoretisch) zu vergewissern, dass
der Begriff der Potenz für beliebige reelle Exponenten einen Sinn macht. Dieses Ziel haben wir erreicht, und so halten wir fest:
| |||||||||||||||||||||||||||||||||||||||||||
|
Für diesen erweiterten Potenzbegriff gelten - neben (1) - auch die anderen Rechenregeln, die wir schon für rationale Exponenten kennengelernt haben. Sie können die wichtigsten mit Hilfe des nebenstehenden Buttons aufrufen. Wir haben damit die Idee der Potenz soweit verallgemeinert, wie das im Rahmen der reellen Zahlen möglich ist. Eine weitere Ausdehnung dieser Idee, nämlich auf komplexe Zahlen, werden wir in einem späteren Kapitel betrachten. |
 komplexe Potenzen (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
Da wir nun beliebige reelle Zahlen als Exponenten verwenden dürfen, können wir fragen, wie die Potenz einer gegebenen (positiven) Basis a von ihrem Exponenten abhängt. Mit anderen Worten, wir können die Zuordnungsvorschrift
betrachten. Sie definiert eine Funktion auf der Menge der reellen Zahlen. Eine derartige Funktion wird Exponentialfunktion genannt. Auch allgemeinere Zuordnungsvorschriften der Form | Funktionen | ||||||||||||||||||||||||||||||||||||||||||
wobei b und c festgehaltene Zahlen sind, werden mit demselben Namen bezeichnet. Exponentialfunktionen spielen in der Mathematik und in vielen ihrer Anwendungen eine wichtige Rolle. Ohne sie ließe sich kaum ein dynamisches System verstehen, sei es physikalischer, chemischer, biologischer oder ökonomischer Natur. Wir werden weiter unten sehen, wie sie dazu benutzt werden, Wachstums- und Zerfallsprozesse zu modellieren. Aber auch in anderen Zusammenhängen begegnen sie uns, von der Wahrscheinlichkeitsrechnung bis zur Quantentheorie. Das Gebiet der Differentialgleichungen wäre ohne sie undenkbar, und ihre Verallgemeinerung im Rahmen der komplexen Zahlen zeigt eine tiefe Verwandtschaft mit Winkelfunktionen und Schwingungsvorgängen auf, deren Anwendungen bis in die Wechselstromtechnik reichen. Diese breite Anwendbarkeit verdanken die Exponentialfunktionen der Einfachheit der ihr zu Grunde liegenden Idee. Lassen wir ihre "Entstehungsgeschichte" kurz Revue passieren: | Dynamische Systeme (in Vorbereitung) Wahrscheinl.rechng (in Vorbereitung) Diff.gleichungen (in Vorbereitung) Winkelfunktionen | ||||||||||||||||||||||||||||||||||||||||||
Machen Sie sich selbst ein wenig mit dem Verhalten der Exponentialfunktionen vertraut! Benuzten Sie etwa den mathe online Funktions-Plotter, um sich die Graphen von 2x, 3x, 10x, (1/2)x, (1/3)x, 2-x und 3-x (einzugeben als 2^x, 3^x, 10^x, (1/2)^x, (1/3)^x, 2^(-x) und 3^(-x)) anzusehen. Weiter unten werden wir die wichtigsten mathematischen Eigenschaften der Exponentialfunktionen besprechen. |
Potenzen | ||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
Wir wollen nun illustrieren, wie Exponentialfunktionen bei der Modellierung von Wachstumsprozessen auftreten. Betrachten wir eine Bakterienkultur. Ihr Wachstum (das aufgrund von Zellteilung zustande kommt) sei durch folgende drei Eigenschaften charakterisiert:
| |||||||||||||||||||||||||||||||||||||||||||
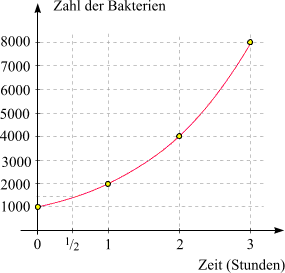
Das ist eine äußerst praktische Formel. Um etwa die Größe der Kultur nach 24 Stunden zu ermitteln, müssen wir nicht 24 Verdoppelungsschritte machen, sondern einfach die Zahl 1000 × 224 berechnen. Wir erhalten 16777216000, d.h. (gerundet) 16.8 Milliarden Stück, also eine sehr große Zahl. Hier sehen wir auch den Grund für die Bezeichnung "exponentiell": Die Zeit-Variable t (die Zahl der vergangenen Stunden) tritt in Formel (4) als Exponent auf. Mit größer werdendem t wächst 2t "exponentiell" an und erreicht sehr schnell riesige Werte. Wie werden in diesem Kapitel des Öfteren auf ähnliche Berechnungen stoßen. Um sie schnell ausführen zu können, stellen wir hier einen Wachstums-Rechner zur Verfügung: Für drei gegebene Zahlen a, b und c berechnet er a × bc. Für die obige Rechnung geben Sie 1000 in das erste, 2 in das zweite und 24 in das dritte (hochgestellte) Textfeld ein und klicken auf das Gleichheitszeichen! (Jeder andere elektronische Rechner oder ein Taschenrechner kann das natürlich auch). Unsere schöne Formel (4) könnte den Anschein erwecken, wir hätten damit bereits ein mathematisches Modell, das das Wachstum der Bakterienkultur in befriedigender Weise beschreibt.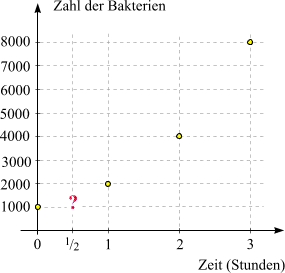 
Im nebenstehenden Diagramm ist dargestellt, was sie leistet: Die Zahl der Bakterien zu einer bestimmten Zeit
wird vertikal über der entsprechenden Zeitmarke aufgetragen. Wird nacheinander
t = 1,
t = 2,
t = 3 usw.
eingesetzt, so liefert Formel (4) die gelben Punkte: die Zahl der zu jeder vollen Stunde vorhandenen Bakterien.
Nun wollen wir aber eine harmlose Frage stellen, und wie so oft in der Mathematik bringen
wir mit einer kleinen Frage große Dinge ins Rollen:
Wie viele Bakterien gibt es nach einer halben Stunde? Wo genau liegt der Punkt
in unserem Diagramm, der der Markierung für 1/2-Stunde
entspricht?Um diese Frage zu beantworten, benötigen wir die Eigenschaft 1 unseres Systems: "In gleich langen Zeitintervallen vergrößert sich die Zahl der Bakterien um den gleichen Faktor". Damit lässt sich das Problem lösen: Nach einer halben Stunde haben sich die Bakterien um einen Faktor vermehrt, den wir im Moment nicht kennen und mit q bezeichnen. 1/2 Stunde nach Beginn gibt es also 1000 q Bakterien. In der darauffolgenden halben Stunde vermehren sie sich - gemäß Eigenschaft 1 - ebenfalls um den Faktor q, d.h. es gibt nun 1000 q2 Bakterien. Andererseits ist insgesamt ist 1 Stunde vergangen, und wir wissen aufgrund von Eigenschaft 3, dass sich die Zahl der Bakterien verdoppelt hat. Es muss also q2 = 2 gelten, woraus q = Ö2 = 1.414213562... folgt. Die Antwort auf die Frage ist also, dass es nach einer halben Stunde (ungefähr) 1414 Bakterien gibt. Der exakte, von unserem Modell vorausgesagte Wert ist 1000 Ö2. Nun beobachten wir, dass das auch als 1000 × 21/2 geschrieben werden kann, denn 21/2 ist gerade die Quadratwurzel aus 2. Das bedeutet aber, dass Formel (4) auch für t = 1/2 gilt ! Eigentlich ist das eine überraschende Erkenntnis! Wir haben Potenzen mit rationalen Exponenten bisher ohne jeglichen Bezug zu konkreten Anwendungen, sondern eher aus formalen Beweggründen heraus - vor allem durch den Wunsch, Rechenregel (1) auch für rationale Exponenten beizubehalten - definiert. Auf keinen Fall haben wir dabei an Bakterien und Wachstumsprozesse gedacht. Und dennoch stellt sich nun heraus, dass sich die Konvention, die Quadratwurzel aus a als a1/2 zu schreiben, bestens zur Beschreibung des Bakterienwachstums eignet. Unser obiger Wachstums-Rechner kennt diese Konvention natürlich auch - probieren Sie es aus, indem Sie 1/2 oder 0.5 in das Textfeld für den Exponenten schreiben! Doch damit nicht genug: Es ist nicht schwer, zu zeigen, dass Formel (4) für alle (positiven) reellen Zeitenangaben t anwendbar ist. Mit anderen Worten:
| |||||||||||||||||||||||||||||||||||||||||||
Um diese Behauptung zu beweisen, kann die
zuvor für t = 1/2
durchgeführte Argumentation auf rationale t verallgemeinert
und die Behauptung anschließend auf reelle t
ausgedehnt werden (siehe den nebenstehenden Button).
Wie werden auf die Frage, warum sich Exponentialfunktionen zur Beschreibung exponentieller Prozesse eignen,
weiter unten noch einmal zurück kommen und den tieferen Grund dafür
- er hängt mit der Rechenregel (1) zusammen -
verstehen.Da t nun einen beliebigen Punkt am positiven Teil der Zahlengeraden darstellen kann, können wir unsere graphische Veranschaulichung des Prozesses verbessern: Die rote Linie im nebenstehenden Diagramm stellt den Graphen der Exponentialfunktion (5) dar. Jetzt sind wir in der Lage, einfache Aufgaben der folgenden Art lösen: Wie groß ist die Anzahl der Bakterien nach einer Stunde und 15 Minuten? Lösung: Eine Stunde und 15 Minuten ist 1.25 Stunden. Wir setzen t = 1.25 in (4) ein und erhalten (z.B. mit Hilfe des obigen Wachstums-Rechners) 2378.41423..., also gerundet: 2378 Stück. Vom mathematischen Standpunkt betrachtet, ist das Interessante aber nicht so sehr das Einsetzen von Zahlen in eine Formel, sondern das Aufstellen von Wachstumsmodellen. Weitere Beispiele exponentieller Wachstumsprozesse Viele Systeme verhalten sich ganz ähnlich wie unsere Bakterien. Wir wollen nun in aller Kürze einige weitere Prozesse vorstellen und zeigen, wie sie in mathematische Form gebracht werden. Für sie alle gelten Eigenschaften analog zu den für das Bakterienwachstum postulierten, wobei Eigenschaft 1 lediglich verbal angepasst, in den Eigenschaften 2 und 3 auch die Zahlenwerte ausgetauscht werden müssen. Zwei Beispiele:
| |||||||||||||||||||||||||||||||||||||||||||
|
Mit Hilfe des nebenstehenden Buttons können Sie eine Liste weiterer Beispiele
aufrufen. In ihr wird die Beschreibungsweise der betrachteten Prozesse ein bisschen variiert, und
es wird vorgeführt, wie die zugehörigen Exponentialfunktionen
ermittelt werden. Unter anderem lernen Sie das
Mooresche Gesetz über die exponentielle Zunahme der Leistungsfähigkeit von Computern kennen.
Als letztes Beispiel wird das Modell für den allgemeinen exponentiellen Wachstumsprozess,
in dem alle Kennzahlen offen gelassen sind, angeschrieben. |
|||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
Nicht nur die Zunahme, sondern auch die Abnahme einer Größe kann auf exponentielle Weise geschehen. Um derartige Prozesse zu beschreiben, ist lediglich eine kleine Änderung unserer bisheigen Betrachtungsweise nötig. Betrachten wir ein radioaktives Präparat, d.h. einen Stoff, in dem eine gewisse Anzahl "zerfallsfähiger" Atomkerne vorhanden sind. Jeder dieser Kerne wird irgendwann "zerfallen", d.h. ein Elementarteilchen (radioaktive Strahlung) aussenden und sich dabei in einen Atomkern nicht-aktiven Typs umwandeln. Je mehr zerfallsfähige Kerne vorhanden sind, umso mehr Strahlung wird emittiert. Da die zerfallsfähigen Kerne nach und nach "verbraucht" werden, wird die Strahlung im Laufe der Zeit abklingen. Die von unserem Präparat ausgehende radioaktive Strahlung sei durch folgende drei Eigenschaften charakterisiert:
abgesunken ist. Das können wir auch als 1000 × (2-1)t schreiben, und da
schreiben. Welche der beiden Formeln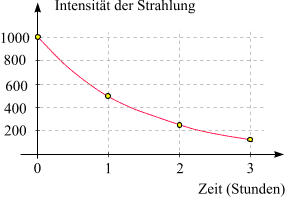 
(6) oder (7) zur Beschreibung des Prozesses benutzt wird, ist
im Grunde genommen gleichgültig. Oft wird die zweite Variante (7) vorgezogen, aber das ist keine
bindende Vorschrift.
Das Minuszeichen im Exponenten zeigt an, dass es sich um einen Zerfalls- und nicht um einen
Wachstumsprozess handelt. Wie im vorigen Abschnitt kann argumentiert werden, dass diese
beiden Formeln für alle (positiven) reellen
t anwendbar sind.
Nebenstehend ist als Veranschaulichung der Graph der Funktion (6) bzw. (7) abgebildet.
Unser obiger Wachstums-Rechner eignet sich
(trotz seines Namens) auch für Zerfallsprozesse.
Probieren Sie es aus, indem Sie die Zahl der Intensität der Strahlung
nach einer Stunde und 15 Minuten (1.25 Stunden) berechnen!Einen Prozess dieses Typs nennen wir exponentiellen Zerfall (Abfall), exponentielle Abnahme oder exponentielles Abklingen. Jene Zeitdauer, während der die beschriebene Größe auf die Hälfte absinkt (in unserem Beispiel: 1 Stunde) heißt Halbwertszeit. Klarerweise handelt es sich bei den gemachten Annahmen (den drei obigen Eigenschaften) wieder nur um ein Modell. Mit wachsendem t fällt 2-t "exponentiell" ab und erreicht schnell sehr kleine Werte. Spätestens wenn kein zerfallsfähiger Atomkern mehr vorhanden ist, ist die Grenze des Modells erreicht. | |||||||||||||||||||||||||||||||||||||||||||
|
Mit Hilfe des nebenstehenden Buttons
können Sie eine Liste weiterer Beispiele für exponentielle Zerfallsprozesse aufrufen.
In ihr wird die Beschreibungsweise der betrachteten Prozesse ein bisschen variiert, und
es wird vorgeführt, wie die zugehörigen Exponentialfunktionen
ermittelt werden. Außerdem erfahren Sie, wie die Altersbestimmung durch die
Radiokarbonmethode funktioniert und wie die Halbwertszeit abgelesen werden kann,
wenn die Exponentialfunktion bekannt ist. Als letztes Beispiel wird
das Modell für den allgemeinen exponentiellen Zerfallsprozessprozess,
in dem alle Kennzahlen offen gelassen sind, angeschrieben. Die Beispiele, verglichen mit jenen des vorigen Abschnitts, illustrieren, dass Wachstums- und Zerfallsprozesse durch denselben Formalismus beschrieben werden: den der Exponentialfunktionen, deren Eigenschaften wir uns im nächsten Abschnitt zuwenden werden. | |||||||||||||||||||||||||||||||||||||||||||
|
|
Dynamische Systeme (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
Wie wir in den beiden vorhergehenden Abschnitten anhand mehrerer Beispiele gesehen haben, ist ein exponentieller Prozess durch eine Exponentialfunktion, d.h. durch eine Funktion der Form (3) definiert. Wir schreiben sie als
Die Wachstums- und Zerfallsfunktionen aller bisher betrachteten Beispiele haben diese Form. Sie unterscheiden sich voneinander lediglich durch unterschiedliche Werte der Konstanten a (> 0), b und c (die auch als Parameter bezeichnet werden). Im Folgenden werden wir einige zentrale Eigenschaften dieser Funktionen diskutieren. Warum sich Exponentialfunktionen zur Beschreibung exponentieller Prozesse eignen Es ist lehrreich, sich kurz zu überlegen, was Funktionen der Form (8) so bedeutend macht. Wir haben exponentielle Wachstums- und Zerfallsprozesse dadurch charakterisiert, dass die betrachtete Größe "in gleich langen Zeitintervallen um den gleichen Faktor wächst (schrumpft)", wobei es nicht immer um zeitliche Abläufe geht, sondern ganz allgemein um das Verhalten einer Größe in Abhängigkeit von einer anderen (wie beispielsweise die Helligkeit des Lichts als Funktion der Dicke einer Glasscheibe, durch die es fällt). Diese entscheidende Eigenschaft findet sich nun bei Funktionen des Typs (8) in der folgenden Form wieder:
Wir können das leicht beweisen, indem wir x + s statt x in (8) einsetzen:
Beim zweiten Gleichheitszeichen haben wir (1), die zentrale Rechenregel für Potenzen, verwendet, beim dritten Gleichheitszeichen haben wir (8) benützt. Diese Identität gilt übrigens für alle reellen s, nicht nur für die positiven. Mit ihr ist die Behauptung bewiesen: Der "Faktor, der nur von s abhängt", ist abs. Wichtig ist, dass er nicht von x abhängt. Mit welchem x auch immer begonnen wird: Wächst x (additiv) um s, so ändert sich der Funktionswert (multiplikativ) um den Faktor abs. Diese Koppelung von additivem mit multiplikativem Verhalten geht auf das Verhalten von Potenzen zurück: den Zusammenhang zwischen dem Produkt (von Potenzen) und der Summe (der Exponenten), wie er durch (1) ausgedrückt wird. Wir sehen also, dass es die Identität (1) ist, der die Exponentialfunktionen ihre Eignung zur Beschreibung exponentieller Prozesse verdanken. Der Rest dieses Abschnitts kann von ''EinsteigerInnen'' ausgelassen werden. Die Rolle der Parameter Die Funktionsterme der Form (8) beinhalten drei Konstante (Parameter) a, b und c. Allerdings sind diese Zahlen durch die Funktion f nicht eindeutig bestimmt! Das liegt daran, dass Potenzen mit verschiedener Basis und verschiedenen Exponenten durchaus dasselbe bedeuten können. So kann beispielsweise 16x/2 auch als 4x oder als 22 x oder auch als (1/2)-2 x geschrieben werden - alle diese Ausdrücke beschreiben ein und dieselbe Exponentalfunktion! Das mag lästig erscheinen, liegt aber in der Natur des Potenzierens. Wir haben also immer die Wahlmöglichkeit zwischen verschiedenen Schreibweisen derselben Exponentialfunktion (zwischen verschiedenen Basen), und wir werden weiter unten eine Regel kennenlernen, wie wir eine Potenz mit irgendeiner Basis zu einer Potenz mit einer beliebigen anderen Basis umformen können. Eine Möglichkeit, einen gegebenen Funktionsterm der Form (8) zu vereinfachen, besteht darin, die Konstante b im Exponenten "zum Verschwinden zu bringen". Das ist gar nicht schwierig, denn wir können (8) in der Form
schreiben, wobei wir A = ab definiert haben. a und b spielen also keine voneinander unabhängige Rolle, sondern es ist nur die Kombination ab, die zählt. Manchmal ist es vorteilhaft, zu wissen, welche Bedeutung die Parameter a, b und c in (8) haben: Wie widerspiegeln ihre Werte die Eigenschaften des modellierten Prozesses? Wir können auch den Spieß umdrehen und fragen, welcher Prozess durch eine gegebene Exponentialfunktion der Form (8) beschrieben wird (wobei wir annehmen, dass a und c positiv sind). Der nebenstehende Button ruft eine Reihe von Bemerkungen zu diesen Fragestellungen auf. | |||||||||||||||||||||||||||||||||||||||||||
|
Definitionsbereich Die Exponentialfunktionen sind für alle reellen Zahlen x definiert, d.h. ihr Definitionsbereich ist die gesamte Menge R. Für die Modellierung eines exponentiellen Prozesses wird in der Regel nur ein Teil dieses Bereichs (üblicherweise x ³ 0) benötigt, da jeder realistische Prozess irgendwann einmal beginnt). Monotonie und Injektivität Zum Abschluss dieses Abschnitts wollen wir noch einige wichtige Eigenschaften der Exponentialfunktionen erwähnen. Wir betrachten Funktionen vom Typ (8) mit c > 0. Sie sind alle positiv: f(x) > 0 für alle x Î R. Mit der Abkürzung A = ab wie in (10) gilt für sie: | Definitionsbereich einer Funktion | ||||||||||||||||||||||||||||||||||||||||||
| Monotonie | ||||||||||||||||||||||||||||||||||||||||||
Aus der Monotonie folgt, dass die betrachteten Funktionen (für c > 0 und A ¹ 1) injektiv sind. Das bedeutet, dass jeder Funktionswert höchstens einmal angenommen wird.
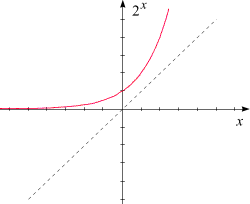
Als letzte Eigenschaft erwähnen wir, dass jede der betrachteten Funktionen (für c > 0 und A ¹ 1) jeden positiven Wert annehmen kann (mit anderen Worten: ihr Wertebereich ist die Menge R+ ): Ihre Graphen nähern sich "im Unendlichen" der x-Achse entweder im Bereich positiver oder negativer x (je nachdem, ob A < 1 oder A > 1 ist) und wachsen im jeweils anderen Bereich über jede Schranke an. Daher wird jede positive Zahl, sei sie noch so klein oder so groß, als Funktionswert angenommen. Um ein Gefühl für diese Eigenschaft zu bekommen, sehen Sie sich einige solcher Graphen (z.B. der Funktionen | Potenzen und die Ordnung der reellen Zahlen injektiv | ||||||||||||||||||||||||||||||||||||||||||
|
Die Exponentialfunktionen besitzen weitere bedeutsame und "schöne" Eigenschaften,
auf die wir in späteren Kapiteln, insbesondere im Rahmen der Differentialrechnung,
stoßen werden. |
Differentialgleichungen (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
Der Schweizer Mathematiker Leonhard Euler hat im 18. Jahrhundert eine Zahl in die Mathematik eingeführt, die mit e bezeichnet wird und seither nicht mehr wegzudenken ist. Wie p ist sie eine irrationale Zahl, und ihre Dezimaldarstellung beginnt mit
Gehört die Eulersche Zahl e nicht zu Ihrem Lernstoff, so überspringen Sie nun den Rest dieses Abschnitts, nehmen aber am Besten zur Kenntnis, dass sie den soeben angeschriebenen Wert hat und als "natürliche Basis" bezeichnet wird. Was es mit der Zahl e auf sich hat, können wir an dieser Stelle nur zu einem kleinen Teil vermitteln, denn ihre Bedeutung wird erst nach und nach mit fortschreitendem Stoff klarer werden. Eine Möglichkeit, die Zahl e kurz und bündig zu definieren, ist diese: e ist die einzige positive Zahl, für die
gilt.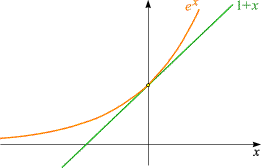 
In der nebenstehenden Skizze sind die Graphen dieser beiden Funktionen gezeichnet:
Jener von ex
liegt - außer im Punkt (0, 1) - gänzlich "oberhalb" der Geraden, die den Graphen von
1+ x bildet.
Die Basis e ist die einzige,
die diese Eigenschaft hat:
Ist a ¹ e,
so schneidet der Graph von ax
die Gerade in zwei Punkten, liegt also zum Teil "unterhalb" von ihr.
Wenn Sie die Maus über die Skizze fühen, so erscheint zum Vergleich der
Graph von 2x; wenn Sie
auf die Graphik klicken, sehen Sie den Graphen von
5x.
Wir wollen diese Veranschaulichung als ausreichende Begründung für die Existenz und
Eindeutigkeit der Zahl e ansehen.
Im nebenstehenden Applet ist sie auf dynamische Weise veranschaulicht.
Mit Hilfe des darunter stehenden Buttons können Sie
einen kleinen Exkurs zur Zahl e
aufrufen, der den soeben beschriebenen Sachverhalt genauer diskutiert. | Zur Definition der Eulerschen Zahl e | ||||||||||||||||||||||||||||||||||||||||||
Wieso ist Eigenschaft (14) bedeutsam?
Das hängt mit der Frage zusammen, wie sich Exponentialfunktionen der Form (2), d.h.
Damit ist gemeint, dass sich für kleine x die beiden Ausdrücke ex und 1+ x nur um eine Zahl unterscheiden, deren Größenordnung noch viel kleiner als x ist. Überprüfen wir das numerisch für x = 0.01: Mit dem Zahlenwert (13) berechnen wir e0.01 = 1.01005016..., was sich von 1 + 0.01 nur um 0.00005016... unterscheidet, und das ist wesentlich kleiner als 0.01 ! Je kleiner x ist, umso besser gilt die Näherung (15). Für andere Basen ist das nicht der Fall: Ist a ¹ e, so gilt für kleine x die Näherungsformel Aus der Definition (14) ergibt sich auch eine Möglichkeit, e zu berechnen. Sie ist im obigen Exkurs genauer begründet. Für den Fall, dass Sie den Exkurs überspringen, wollen wir diese Methode (ohne Beweis) kurz skizzieren:
| Grenzwert (in Vorbereitung) Potenzreihen (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||||||
|
e als natürliche Basis Was das Verhalten für kleine x betrifft, ist, wie wir gesehen haben, e unter allen Basen für Potenzen als die "schönste" anzusehen. Sie wird deshalb auch die natürliche Basis genannt. Die Funktion
Diese Schreibweise empfiehlt sich insbesondere dann, wenn anstelle von x ein längerer Term steht. Wird in einem mathematischen Text von der Exponentialfunktion gesprochen, so ist meistens diese Funktion gemeint. Sie können den obigen Wachstums-Rechner benutzen, um Potenzen der natürlichen Basis numerisch zu ermitteln, indem Sie die Zahl 1 in das erste und den Buchstaben E - für e - in das zweite Textfeld eingeben. In vielen Anwendungen ist es üblich, für Exponentialfunktionen generell die Basis e zu verwenden. Insbesondere werden (z.B. radioaktive) Zerfallsprozesse in der Physik meist in der Form
angeschrieben, wobei f die betrachtete Größe (z.B. die Strahlungs-Intensität) bezeichnet, t für die Zeit steht und l Zerfallskonstante (manchmal auch Zerfallsrate) heißt. Deren Zusammenhang mit der Halbwertszeit werden wir weiter unten behandeln. Analog werden Wachstumsprozesse oft in der Form | Rate (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||
|
Zuletzt noch eine Bemerkung zur Zahl e auf elektronischen Rechnern: Falls Ihr Taschenrechner keine eigene Taste für e besitzt, aber eine für die Exponentialfunktion zur natürlichen Basis (als ex oder exp gekennzeichnet), kann e als e1 oder exp(1) angesprochen werden. In manchen computerbasierten Rechenprogrammen (insbesondere in den auf JavaScript beruhenden, wie der mathe online Mini-Rechner und JavaCalc) muss e als Grossbuchstabe E eingegeben werden. Die Zahl e wird uns in späteren Kapiteln wieder begegnen. |
Wahrscheinl.rechnung (in Vorbereitung) Komplexe Zahlen (in Vorbereitung) Dynamische Systeme (in Vorbereitung) Differenzieren 1 | ||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
Wir wählen eine Basis a > 0 (a ¹ 1) und betrachten die durch (2) definierte Exponentialfunktion
gilt. Mit anderen Worten: Die Gleichung (19) hat genau eine Lösung für x. Beispiele: Die Gleichung 3x = 9 hat die (eindeutige) Lösung x = 2. Die Gleichung 16x = 4 hat die (eindeutige) Lösung x = 1/2. Die Gleichung (1/2)x = 8 hat die (eindeutige) Lösung x = -3. Was aber ist die (eindeutige) Lösung der Gleichung 3x = 8? Sie wird ein bisschen kleiner als 2 sein, aber können wir Genaueres über sie aussagen? Leider bringen uns die Rechenoperationen, die wir bisher kennengelernt haben, hier nicht weiter! Die gesuchte Lösung ist eine irrationale Zahl, die nicht als Bruchzahl, Wurzel oder dergleichen dargestellt werden kann. Wir können uns allerlei Näherungsverfahren ausdenken, um sie numerisch zu berechnen. Momentan ist es für uns aber wichtiger, einen mathematisch genauen Begriff von ihr zu haben. Daher geben wir ihr zunächst einen Namen: Wir nennen sie den "Logarithmus von 8 zur Basis 3". Ganz allgemein legen wir fest:
Statt alog b werden manchmal auch die Bezeichnungsweisen alog b oder loga b verwendet. Um die numerische Berechnung von Logarithmen müssen wir uns keine Sorgen machen - das tun Werkzeuge wie der Taschenrechner oder der Computer für uns. (Die Art und Weise, wie Rechenmaschinen das machen, werden wir in diesem Kapitel nicht kennenlernen). Für den praktischen Gebrauch stellen wir hier einen Log-Rechner zur Verfügung: Probieren Sie ihn gleich aus und berechnen Sie die Lösungen der zuvor als Beispiele angeführten Gleichungen: 3log 9, 16log 4, 1/2log 8 und 3log 8. Letzteres beantwortet die Frage nach der Lösung der Gleichung 3x = 8. Was sollen wir uns unter dem Logarithmus vorstellen? Das "Logarithmieren" ist die "Umkehrung des Potenzierens". Die Berechnung von alog b enspricht der Frage: Mit welchem Exponenten kann b als Potenz von a dargestellt werden, d.h. für welches x gilt b = ax? Salopper ausgedrückt, könnte man formulieren: Wie oft muss die Basis a "mit sich selbst multipliziert" werden, um b zu ergeben? Dieser Sachverhalt lässt sich am einfachsten anhand der Basis 10, die der Dezimaldarstellung der reellen Zahlen zu Grunde liegt, verdeutlichen: So ist 10log 1000 = 3, da sich 1000 als 103 darstellen lässt: 10log 1000 ist die Anzahl der in der Dezimaldarstellung von 1000 vorkommenden Nullen, nämlich 3. Dass 10log 0.01 = -2 ist, rührt daher, dass die Zahl 0.01 als "Zehnerpotenz" 10-2 dargestellt werden kann. Die Beziehung 10log 1500 = 3.17609... gilt deshalb, weil die Zahl 1500 als "Zehnerpotenz" 103.17609... darstellbar ist. Aufgrund dieser Eigenschaft, den Exponenten einer Zehnerpotenz anzugeben, eignet sich der Logarithmus zur Basis 10 gut als Maß für die Angabe großer Zahlen: So liegt er beispielsweise für eine Zahl, deren Dezimaldarstellung (vor dem Komma) 54 Stellen hat (die also enorm groß ist), zwischen 53 und 54. Insofern beruht er auf der Idee, die "Anzahl der Dezimalstellen" als Größenmaß zu verwenden. Er wird oft verwendet, wenn in einem Problem Zahlen auftreten, die mehrere Zehnerpotenzen umfassen. Logarithmusfunktionen Wir können den Logarithmus auch in funktionstheoretischen Begriffen fassen: Jede Exponentialfunktion | R+ Umkehrfunktion | ||||||||||||||||||||||||||||||||||||||||||
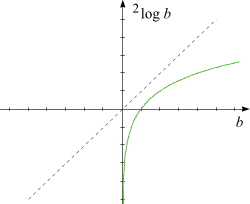
Diese Charakterisierung sagt uns unmittelbar, wie der Graph der Logarithmusfunktion zu einer
gegebenen Basis a
aus jenem der entsprechenden Exponentialfunktion gewonnen werden kann:
Fassen wir in Gleichung (19) die Zahl b
als abhängig von x auf, so können wir die Exponentialfunktion als
anschreiben. Nun denken wir uns diese "Gleichung" nach x
aufgelöst: Die (eindeutige) Lösung x
hängt von der Zahl b ab, so dass die Logarithmusfunktion in der Form
mit horizontaler b-Achse und
vertikaler x-Achse eingezeichnet.
Die beiden Koordinatensysteme unterscheiden sich nur dadurch voneinander, dass die Achsenbezeichnungen
vertauscht sind. Da beide Graphen denselben Zusammenhang darstellen, müssen sie ineinander übergehen,
wenn x und b vertauscht werden.
Nun entspricht die Überführung eines Punktes mit Koordinaten
(x, b)
in einen Punkt mit Koordinaten
(b, x)
gerade einer Spiegelung um die erste Mediane, d.h. um die 45°-Gerade, auf der
b = x gilt.
Wir schließen, dass der Graph der Logarithmusfunktion aus dem Graphen der Exponentialfunktion durch
Spiegelung an der ersten Mediane hervorgeht.
Die beiden Skizzen illustrieren das für die Basis a = 2
(wobei die erste Mediane strichliert dargestellt ist).
Die Graphen für andere Basen a > 1
sehen ähnlich aus.
Können Sie an dieser Stelle selbst herausfinden, wie die Graphen der Logarithmusfunktionen zu Basen a < 1
aussehen? (Wir werden auf diese Funktionen weiter unten zu sprechen
kommen).
| Mediane | ||||||||||||||||||||||||||||||||||||||||||
|
Spezielle Basen Einige Basen werden besonders oft verwendet:
| |||||||||||||||||||||||||||||||||||||||||||
|
Wie Sie sehen, ist die Bedeutung des Symbols "log" nicht einheitlich geregelt. Falls Sie es in einem mathematischen
Text oder Werkzeug antreffen, informieren Sie sich bitte im Zweifelsfall immer,
um welchen Logarithmus es sich dabei handelt.
Definitionsbereich und Monotonie-Eigenschaften des Logarithmus Dieser Unter-Abschnitt kann von ''EinsteigerInnen'' ausgelassen werden. Da der Logarithmus und die Exponentialfunktion Umkehrfunktionen voneinander sind, übertragen sich die Eigenschaften und Rechenregeln der einen auf die andere. Zuerst betonen wir nochmals, dass die Funktion alog, d.h. die Zuordnung | komplexe Zahlen (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||||||
|
Eine weitere Eigenschaft des Logarithmus, die er von der Exponentialfunktion geerbt hat, können wir anhand des oben dargestellten Graphen der Funktion 2log erkennen:
Rechenregeln für den Logarithmus Die Definition des Logarithmus kann in der Identität
zusammengefasst werden: Kann eine Zahl (in der obigen Definition b genannt) in der Form ax geschrieben werden, so ist ihr Logarithmus (zur Basis a) gleich x. Hier kommt noch einmal die Bedeutung des Logarithmus als Exponent zum Ausdruck! Setzen wir x = 1, so erhalten wir die Identität Die wichtigste Rechenregel für den Umgang mit Logarithmen entsteht unmittelbar aus der Identität (1) für das Rechnen mit Potenzen (die, wie wir oben begründet haben, auch für reelle Exponenten gilt). Ihre Herleitung ist eine gute Übung im Umgang mit dem Logarithmusbegriff: Wir fixieren zunächst eine Basis a > 0 (a ¹ 1). Weiters betrachten wir zwei beliebige positive Zahlen b, c und bezeichnen deren Logarithmen als x = alog b und y = alog c. Das bedeutet, dass ihre Darstellung als Potenzen von a die Form b = ax und c = a y hat. Nun kann das Produkt
für alle b, c > 0. In Worten: Der Logarithmus eines Produkts ist gleich der Summe der Logarithmen. Diese schöne Identität kann als "Umkehrung" der Regel (1) betrachtet werden, und in erster Linie ihr verdankt der Begriff des Logarithmus seine Bedeutung. | |||||||||||||||||||||||||||||||||||||||||||
|
Wir erwähnen noch zwei weitere Rechenregeln:
für alle b, c > 0 und beliebige reelle k. Als wichtiger Spezialfall ergibt sich daraus (entweder mit k = -1 in der ersten oder mit b = 1 in der zweiten Identität)
für alle b > 0. Intuitiv sind alle diese Rechenregeln leicht zu erfassen, wenn Sie sie anhand Zehner-Logarithmus und "runder" Zehnerpotenzen durchspielen. So ist etwa lg 100 = 2 (die "Zahl der Nullen") und lg 1000 = 3, daher lg 100000 = 5 = 2 + 3. In diesem Beispiel reduziert sich die Identität (22) auf das Abzählen von Nullen. | |||||||||||||||||||||||||||||||||||||||||||
|
Mit Hilfe der Identitäten (21)-(25) können wir viele nützliche Aspekte des Logarithmus verstehen:
von der logarithmischen Skala (dem logarithmischen Maßstab)
und ihrer Bedeutung für die Darstellung von Funktionsgraphen und funktionalen Abhängigkeiten
über das Logarithmenpapier und
die legendären Logarithmentafeln, die Jahrhunderte lang die Basis numerischer Berechnungen
bildeten, bis zum fast schon vergessenen Rechenschieber (Rechenstab).
Mit Hilfe des nebenstehenden Buttons
können Sie einen kleinen Exkurs über diese Themen aufrufen. Weiters sind wir nun in der Lage, Ausdrücke, die Logarithmen beinhalten, zu vereinfachen. Beispiel: Vereinfachen Sie den Term Umrechnen von Basen Dieser Unter-Abschnitt kann von ''EinsteigerInnen'' ausgelassen werden. Exponential- und Logarithmusfunktionen werden zwar auf eine Basis bezogen, aber wir haben schon oben bemerkt, dass die Basis nicht eindeutig ist. 16x/2 (Basis 16) ist dasselbe wie 4x (Basis 4). Tatsächlich können wir jede Exponentialfunktion auf jede Basis beziehen. Der Logarithmusbegriff gibt uns die Möglichkeit, das rechnerisch durchzuführen. Weiters können Logarithmen zu verschiedenen Basen ineinander umgerechnet werden. | |||||||||||||||||||||||||||||||||||||||||||
Die beiden Identitäten, die das bewerkstelligen, sind:
Da sie eine etwas unübersichtliche Struktur haben, konkretisieren wir sie, indem wir c = e setzen. Das entspricht dem Problem, eine Potenz ax und einen Logarithmus alog b auf die natürliche Basis umzuschreiben:
Wir sehen, dass die Umrechnung gar nicht so kompliziert ist: In beiden Fällen ist einfach an geeigneter Stelle der "Umrechnungsfaktor" ln a (in den die alte und die neue Basis eingehen) einzufügen. Die erste dieser Umrechnungsformeln, (28), dient beispielsweise dazu, einen in der Form Die zweite Umrechnungsformel, (29), kann unter anderem dann nützlich sein, wenn Sie ein Computerwerkzeug benutzen, das - wie es häufig der Fall ist - nur den natürlichen Logarithmus unterstützt. Benutzen Sie sie, um sich mit Hilfe des mathe online Funktions-Plotters die Graphen einiger Logarithmen zu verschiedenen Basen (beispielsweise 1/2, 2, 10) anzusehen! Beachten Sie: Die in diesem Werkzeug als log bezeichnete Funktion stellt den natürlichen Logarithmus dar. Um etwa den Graphen des Logarithmus zur Basis 2 darzustellen, geben Sie die Funktion log(x)/log(2) ein. Logarithmus am Computer Wie bereits oben erwähnt, sind die Bezeichnungen für die verschiedenen Logarithmen sind nicht einheitlich geregelt. Manche elektronische Werkzeuge (insbesondere die auf JavaScript basierten, wie der mathe online Mini-Rechner und JavaCalc, aber auch der mathe online Funktions-Plotter) unterstützen nur den natürlichen Logarithmus, und dieser ist unter der Bezeichnung log verfügbar. Mit Hilfe der Identität (29) können Sie damit auch Logarithmen zu anderen Basen ansprechen. | |||||||||||||||||||||||||||||||||||||||||||
|
|
Differenzieren 1 * komplexe Zahlen (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
Der Begriff des Logarithmus erlaubt die Lösung von Aufgabenstellungen, die bei Wachstums- oder Zerfallsprozessen typischerweise auftreten. Wir wollen das anhand zweier Beispiele besprechen: Beispiel 1: Eine Kultur von ursprünglich 1000 Bakterien wächst exponentiell und verdoppelt ihre Größe jede Stunde. Zu welcher Zeit weist sie 7000 Bakterien auf?
| |||||||||||||||||||||||||||||||||||||||||||
Beispiel 2: Die Intensität eines radioaktiven Stoffs fällt in 5 Jahren auf 1/3 ihres ursprünglichen Werts ab. Wie groß ist die Halbwertszeit, d.h. in welcher Zeit ist die Intensität auf die Hälfte abgesunken?
In den Gleichungen (30) und (33) ist die Unbekannte im Exponenten aufgetreten, und der Logarithmus war ein Mittel, sie zu lösen. Manchmal treten auch Gleichungen wie
| Äquivalenz- umformungen | ||||||||||||||||||||||||||||||||||||||||||
|
auf, die von Beginn an Logarithmen enthalten. Um diese Gleichung zu lösen, bemerken wir zunächst, dass sie nur dann einen Sinn macht, wenn x2 und x + 1 positiv sind. Die Definitionsmenge der Gleichung ist daher
entsteht. Da der Logarithmus eine injektive Funktion ist, müssen die Argumente gleich sein:
was sich nach dem Auflösen der Klammer als lineare Gleichung mit Lösung x = -1/2 herausstellt. Da dieser Wert in der Definitionsmenge enthalten ist, haben wir damit die (einzige) Lösung der Gleichung (36) gefunden. | Definitionsmenge einer Gleichung | ||||||||||||||||||||||||||||||||||||||||||
|
Mit diesen Methoden haben wir die Klasse der uns zugänglichen Gleichungen erheblich vergrößert.
Zur Warnung sei jedoch hinzugefügt, dass sich nicht jede Gleichung, die
Potenzen oder Logarithmen der Unbekannten enthält, auf diese Weise behandeln lässt.
So kann es geschehen, dass eine derartige Gleichung zwar Lösungen besitzt, die sich aber nicht durch
Potenzen, Logarithmen oder irgendwelche anderen uns bisher bekannten
Rechenmethoden (in "geschlossener" Form, wie es heißt) ausdrücken lassen.
In einem solchen Fall bleibt nur mehr der Griff zu graphischen oder numerischen
Näherungs-Techniken. Ein Beispiel stellt die Gleichung
| graphisches Lösen von Gleichungen | ||||||||||||||||||||||||||||||||||||||||||
|
Zum Abschluss möchten wir Sie noch darauf hinweisen, dass das auf Mathematica beruhende Online-Werkzeug |
|||||||||||||||||||||||||||||||||||||||||||
|
|
||
|
|
Zum Seitenanfang Zum Lexikon Zur Galerie Zum Kapitel Exponentialfunktion und Logarithmus der Galerie Zum Inhaltsverzeichnis der Mathematischen Hintergründe Zu den interaktiven Tests Zu den Mathe-Links und Online-Werkzeugen Zur Welcome Page |
