|
|
| |||||||||||||||||||||||||||||||||||||||||||||||
|
Die Bedeutung zweidimensionaler Betrachtungen in der Mathematik rührt zunächst daher, daß ihre Anfänge mit Problemen der Landvermessung verbunden waren. Weiters hat die Ebene gegenüber dem Raum einen Vorteil: In ihr kommen "ideale" mathematische Objekte unseren Handlungsmöglichkeiten sehr nahe: Wir können Punke, Strecken, Kreise, Dreiecke und andere geometrische Figuren zeichnen, anhand von Skizzen und Zeichnungen Längenverhältnisse studieren, Zusammenhänge entdecken (zum Beispiel den Lehrsatz des Pythagoras oder die Tatsache, daß die Winkelsumme im Dreieck 180° ist), mit einem Wort: Mathematik betreiben. |  Satz des Pythagoras, Winkelsumme im Dreieck (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||||||||||
|
Die mathematische Ebene kann man sich als Idealbild eines Blatt Papiers vorstellen, so glatt, daß sich auf ihr kein Ort vom anderen unterscheidet, so eben, daß sich auf ihr keinerlei Berge oder Täler finden, unendlich ausgebreitet ohne Grenze nach allen Richtungen. Sie ist ohne Dicke, ohne Farbe und ohne Geruch. Sie besteht aus Punkten, die nicht einfach sehr klein sind, sondern überhaupt keine Ausdehnung haben. Und aus diesen Punkten wiederum bestehen die geometrischen Figuren, die seit einigen tausend Jahren die Menschen beschäftigt und begeistert haben. Wenn wir an eine solche Ebene denken, denken wir unwillkürlich ans Zeichnen, und daher nennen wir sie Zeichenebene. | |||||||||||||||||||||||||||||||||||||||||||||||
|
Ebenso wie die Zeichenebene sind auch die Punkte, Geraden, Kreise und alle anderen geometrischen Figuren, die sie bevölkern, gedankliche Idealisierungen. So besteht zum Beispiel eine Kreislinie in der Zeichenebene aus allen Punkten, die von einem gegebenen Punkt (dem Mittelpunkt) denselben Abstand (Radius) haben. Eine solche Kreislinie hat keine Dicke. (Oft wird gesagt, sie ist "unendlich dünn"). Ihr Radius ist eine reelle Zahl und kann frei vorgegeben werden. Eine reelle Zahl kann - als Dezimalzahl angeschrieben - unendlich viele von Null verschiedene Ziffern hinter dem Komma besitzen. In ihr steckt also eine gewaltige Menge an Information (wohingegen der Radius eines realen Objekts wie einer Kreislinie, die Sie mit dem Zirkel zeichnen, aufgrund der Dicke des Strichs und aufgrund kleiner Unregelmäßigkeiten nur auf wenige Stellen genau bestimmt ist). |  reelle Zahlen | ||||||||||||||||||||||||||||||||||||||||||||||
| Um ein anderes Beispiel zu nennen: Ist die Größe eines Quadrats durch die Angabe seiner Seitenlänge (d.h. einer reellen Zahl) eindeutig bestimmt, so ist auch die Länge seiner Diagonale eine ganz bestimmte reelle Zahl, die sich durch Vermessungen von realen quadratischen Objekten nie so genau bestimmen läßt wie durch eine mathematische Überlegung. All dies führt dazu, daß in der Mathematik ist ein sehr strenger Begriff von Genauigkeit (Exaktheit) möglich ist. Darüber werden wir in einem anderen Kapitel mehr sagen. |  (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||||||||||
|
Die Zeichenebene und ihre Objekte (genauer: ihre Teilmengen) sind also hochgradig idealisierte Angelegenheiten, Abstraktionen. Dennoch sind die Vorstellungen, die wir mit einem Blatt Papier, einem gut gespitzten Bleistift, einem Lineal und einem Zirkel verbinden, wertvoll, und sie werden uns nützliche Dienste erweisen. |  Teilmenge | ||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||
|
Für viele Zwecke ist es notwendig, ein Orientierungssystem auf der Zeichenebene zur Verfügung zu haben. Dazu denken wir uns zwei aufeinander normal stehende Gerade gezeichnet. Wir betrachten die Ebene mit unserem geistigen Auge so, daß wir eine der beiden Geraden horizontal sehen, die andere vertikal. (Wir verwenden diese Begriffe in der Bedeutung, die sie haben, wenn über ein Blatt Papier gesprochen wird). Den beiden Geraden geben wir nun Namen: Die erste nennen wir x-Achse, die zweite y-Achse (wobei die Symbole x und y häufig verwendet werden, aber auch durch andere ersetzt werden können. Die erste Achse wird Abszisse, die zweite Ordinate genannt). Wir sprechen von Koordinatenachsen oder kurz Achsen.
Zuletzt geben wir ihnen - gemäß folgender Skizze - je eine
"Richtung", die durch einen Pfeil angedeutet ist:
 Damit ist gemeint, daß die Achsen ohne Begrenzung "bis ins Unendliche" laufen (obwohl wir natürlich nur einen endlich großen Ausschnitt der Ebene zeichnen können). Die beiden Achsen schneiden einander in einem Punkt, den wir Ursprung nennen.
Diese Konstruktion versetzt uns in die Lage, die Position von Punkten in Form von Zahlen angeben
zu können.
Nehmen wir an, P sei ein Punkt auf der
Zeichenebene. Dann zeichnen wir die Abstände zu den beiden Achsen wie in der folgenden Skizze ein
(wobei wir den Achsen Markierungen im Abstand 1 geben, um Längen leichter ablesen zu können):
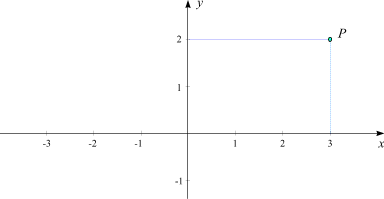 Die beiden Abstände in diesem Beispiel sind 3 und 2. Die erste Zahl - also 3 - nennen wir die x-Koordinate, die zweite Zahl - also 2 - nennen wir die y-Koordinate des Punktes P. Diese beiden Zahlen bestimmen die Position des Punktes (in Bezug auf die Achsen) eindeutig. Genau genommen funktioniert dieses Methode der Positionsbestimmung nur, wenn der Punkt rechts von der y-Achse und oberhalb der x-Achse liegt. Im allgemeinen Fall müssen wir auch negative Koordinatenwerte zulassen: 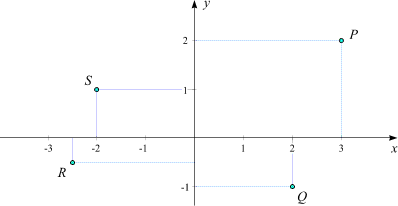 Die eingezeichneten Punkte haben folgende Koordinaten:
Spezialfälle:
Bisher haben wir Koordinaten (bis auf ihr Vorzeichen) als Abstände von den Achsen betrachtet. Es gibt aber noch eine andere nützliche Art, sich Koordinaten vorzustellen. Wir können die Koordinaten eines Punktes als Anweisung betrachten, wie man vom Ursprung ausgehend zu ihm gelangt, genauso wie bei einer Schatzsuche:
Wir können auch den Spieß umdrehen und vom Ursprung aus zuerst nach oben oder unten und dann nach rechts oder links gehen, um zum selben Punkt zu gelangen. Der Grund dafür liegt darin, daß sich in den Skizzen, die bisher gezeigt wurden, Rechtecke verbergen.
Hier ein Beispiel:
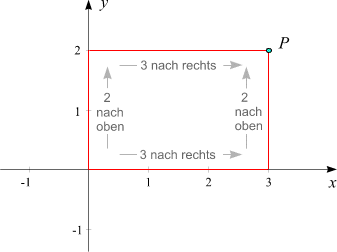 Die Geschichte mit der Schatzsuche kann dazu benützt werden, um auf einem Blatt Papier einen Punkt, dessen Koordinaten gegeben sind, einzuzeichnen: Üblicherweise wird
Die Pfeile geben jeder Achse eine "Orientierung". Sie zeigen jene Richtungen an, in die die Koordinaten anwachsen: Wird ein Punkt
Die Orientierung der Achsen bringt eine besondere Sprechweise mit sich:
Jene "Hälfte" der x-Achse,
die vom Ursprung aus in die positive Richtung (d.h.in Richtung des Pfeils) verläuft,
wird (etwas schlampig)
positive x-Achse
genannt, und entsprechend spricht man von der
negativen x-Achse, der
positiven y-Achse und der
negativen y-Achse.
Um die Vorzeichenkombinationen der Koordinaten von Punkten bequem angeben zu können, werden vier Quadranten ("Viertelebenen") unterschieden, wobei im Gegenuhrzeigersinn von 1 (erster Quadrant) bis 4 (vierter Quadrant) gezählt wird:
Koordinaten der Art, wie wir sie hier beschrieben haben, heißen kartesische Koordinaten (nach René Descartes, 1596 - 1650, der die Bedeutung der Koordinatensysteme für die moderne Mathematik erkannte und seinen Namen nach einer Mode seiner Zeit in die lateinische Form Cartesius abänderte) oder rechtwinkelige Koordinaten (da die beiden Achsen im rechten Winkel zueinander stehen). Die beiden Achsen, zusammen mit ihren Orientierungen (den Pfeilen) bilden ein (kartesisches oder rechtwinkeliges) Koordinatensystem. Sein Sinn ist es also, uns eine Vorschrift in die Hand zu geben, wie die Position eines Punktes durch zwei Zahlen (den Koordinaten) ausgedrückt werden kann. Dadurch werden viele geometrische Probleme einer rechnerischen Behandlung zugänglich gemacht.
Achtung: Die Bezeichungen x
und y werden zwar häufig verwendet
(man spricht dann von einem xy-Koordinatensystem),
sind aber nicht obligatorisch. Man könnte an ihrer Stelle irgendwelche anderen Symbole verwenden.
Heißen die Koordinaten beispielsweise
r und
s, so sprechen wir
von einer r-Achse und einer
s-Achse
(die erste wieder Abszisse, die zweite Ordinate genannt)
bzw. von einem rs-Koordinatensystem,
und davon abgesehen wäre alles genauso wie hier beschrieben.
| |||||||||||||||||||||||||||||||||||||||||||||||
|
Im nebenstehenden Applet können Sie einen Punkt auf der Zeichenebene bewegen und seine Koordinaten ablesen. Es kann Ihnen dabei helfen, zu verstehen, was Koordinaten sind. Der interaktive Test Koordinaten ablesen gibt Ihnen zusätzliche Übungsmöglichkeiten. | Kartesische Koordinaten | ||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||
|
Die Position jedes Punktes in der Zeichenebene kann durch die Angabe zweier reeller Zahlen (seiner Koordinaten) beschrieben werden. Nehmen wir beispielsweise an, die x-Koordinate eines Punktes P sei 3, seine y-Koordinate sei 2. Diese beiden Zahlen werden üblicherweise zu einem Zahlenpaar zusammenfaßt, das in der Form |  Zahlenpaar | ||||||||||||||||||||||||||||||||||||||||||||||
Um auszudrücken, daß der Punkt
P die Koordinaten
Um Punkten Namen zu geben, werden meistens Großbuchstaben verwendet. So
sagt etwa die Angabe | |||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||
|
Ausgehend von einzelnen Punkten, können beliebige geometrische Figuren in einer Sprache charakterisiert und beschrieben werden, die nur Zahlen benützt. Wir beschränken uns hier auf die einfachsten Dinge. Sind etwa die Punkte P und Q durch ihre Koordinaten eindeutig festgelegt, so ist auch die Strecke zwischen ihnen ein eindeutiges (exakt festgelegtes) geometrisches Objekt. Sie wird üblicherweise als PQ bezeichnet. Wir können nun die beiden Punkte und die Strecke, die sie verbindet, in eine Skizze einzeichen. Obwohl jede reale Zeichnung von Ungenauigkeiten (wie zum Beispiel der Strichdicke) gekennzeichnet ist, meinen wir damit "ideale" (also mathematische) Objekte. Genau diese mathematischen Objekte werden durch die Angabe der Koordinaten der Punkte P und Q in exakter Weise charakterisiert. Um einen Geschmack davon zu bekommen, wie die Angabe von Koordinaten mit mathematischen Fragestellungen zusammenhängt, nehmen wir an, wir legen zwei Strecken durch die Koordinaten ihrer Endpunkte fest. Nehmen wir weiters an, daß diese beiden Strecken "einander schneiden", d.h. einen gemeinsamen Punkt besitzen. Er wird Schnittpunkt genannt, und es läßt sich nun fragen, wo er liegt.
Beispiel: Gegeben seien die vier Punkte
Die Angabe reicht aus, um auf einem Blatt Papier eine Skizze der Situation zu machen. Der Schnittpunkt der beiden Strecken ist zeichnerisch leicht ermittelt. Um aber exakt anzugeben, wo er liegt, ist es am einfachsten, seine Koordinaten zu ermitteln. | |||||||||||||||||||||||||||||||||||||||||||||||
| Mit Hilfe des nebenstehenden Applets können Sie das Einzeichnen von Punkten und das Ablesen von Koordinaten (insbesondere der Koordinaten von Schnittpunkten) üben. | Zeichenebene und Koordinatensystem | ||||||||||||||||||||||||||||||||||||||||||||||
|
Wir werden später Methoden kennenlernen, mit deren Hilfe solche Problemstellungen rechnerisch gelöst werden können. |  Analytische Geometrie 1 (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||
|
Dieser Abschnitt kann von ''EinsteigerInnen'' ausgelassen werden. Die Idee der Koordinaten ist nicht nur nützlich, um die Position von Punkten in Zahlen zu fassen. Sie erlaubt uns, einen genaueren Begriff der Zeichenebene zu entwickeln. Wir haben die Zeicheneben oben als "Idealbild" eines Blatt Papiers bezeichnet, eben und unendlich ausgebreitet, ohne Dicke, ohne Farbe und Geruch usw. Das ist natürlich keine besonders mathematische Charakterisierung - sie ist eher philosophischer Natur.
Die Koordinaten erlauben uns nun einen Blick aufs Wesentliche: Die Zeichenebene ist die Menge aller
in ihr liegenden Punkte. Ist nun ein (kartesisches) Koordinatensystem festgelegt, so kann
jeder Punkt durch ein Zahlenpaar (das aus seinen Koordinaten besteht) dargestellt werden.
Und außer der Tatsache, daß er irgendwo in der Zahlenebene liegt, hat ein (mathematischer) Punkt eigentlich
keine weiteren Eigenschaften! Ein Zahlenpaar
Wir könnten noch zugespitzter sagen: Ein Punkt der Zeichenebene ist ein Paar reeller Zahlen. Damit sind all die Eigenschaften, die "kleine Objekte" der realen Welt besitzen können, abgestreift. Wenn wir uns auf die Sprachregelung einigen, daß ein Punkt einfach ein Zahlenpaar ist, brauchen wir keine zusätzlichen philosophischen Anstrengungen zu unternehmen wie "hat keinerlei Ausdehnung" und auch "sonst keine weitere Eigenschaft". Diese Reduktion auf das vom mathematischen Standpunkt Wesentliche ist eine gedankliche Abstraktion, aber nun ist es eine, mit der wir auf formale und präzise Weise umgehen können. Von diesem Standpunkt aus betrachtet, stellt sich die Zeichenebene - die Menge aller in ihr liegenden Punkte - als Menge aller reellen Zahlenpaare heraus. Die Menge der reellen Zahlen wird mit R bezeichnet, die Menge aller Paare von reellen Zahlen als R2 (ausgesprochen als "R zwei"). Wir sind dieser Menge bereits in einem früheren Kapitel begegnet. In der mathematischen Formelsprache ist sie durch
|  der Menge R2  Mengen- schreibweise | ||||||||||||||||||||||||||||||||||||||||||||||
|
Wir identifizieren also die Zeichenebene mit der Menge
R2.
Wir könnten noch zugespitzter sagen: Die Zeichenebene ist die Menge
R2.
Von diesem Standpunkt aus betrachtet ist es nicht mehr notwendig, die Zeichenebene als
"ohne Dicke" und "unendlich ausgebreitet" zu beschreiben, denn das alles erhalten wir nun
gratis mitgeliefert: Mit der Menge R2
ist weder eine Dicke verbunden, noch hat sie eine Grenze, noch eine Farbe oder einen
Geruch. Und - es läßt sich über sie auf präzise Weise sprechen.
Genau das wünschen wir uns in der
Mathematik.
Wir sollten die Sache mit dem Blatt Papier (die "Vorlage" der Abstraktion, an der wir nun angelangt sind)
dennoch nicht zur Gänze vergessen, denn sie ist nach wie vor nützlich,
um sich unter der Zeichenebene
etwas vorzustellen.
Fassen wir zusammen:
Hier ist allerdings noch eine kleine Anmerkung zu machen: Die Zeichenebene "als solche" ist nicht mit einem Koordinatensystem ausgestattet. Wir haben ein solches konstruiert, indem wir uns (in Gedanken) zwei aufeinander normal stehende Achsen ausgedacht haben und ihnen Richtungen (Pfeile) gegeben haben (siehe oben). Dementsprechend haben wir der Ebene einen "Mittelpunkt" gegeben: den Ursprung, der jetzt - als Element von R2 - einfach das Zahlenpaar |  Mathematische Strukturen und Räume (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||||||||||
Für praktisch alle Zwecke der Schulmathematik spielt dies jedoch glücklicherweise keine Rolle. Wir können uns vorstellen, ein Koordinatensystem sei fix gewählt, und in Bezug auf dieses wird die Zeichenebene mit dem R2 identifiziert. | |||||||||||||||||||||||||||||||||||||||||||||||
|
In einem früheren Kapitel wurde übrigens bereits die Idee
des Koordinatensystems verwendet, ohne daß sie so benannt wurde:
Die Zahlengerade besteht in der Vorstellung, die Position von Punkten
auf einer Linie (einem "eindimensionalen" Gebilde) durch reelle Zahlen zu beschreiben.
Über die ("zweidimensionales") Ebene sprechen wir hier.
Analog dazu kann die Position von Punkten im ("dreidimensionalen")
Raum mit Hilfe von drei Zahlen beschrieben werden, wodurch dieser
mit der Menge R3 aller
reellen Zahlentripel identifiziert wird.
Dadurch gewinnen wir einen Zugang zu höherdimensionalen Räumen,
wie beispielsweise dem "vierdimensionalen"
R4 als Menge aller reellen
"Zahlen-4-Tupel". Der läßt sich nicht mehr so gut vorstellen wie
Linien, Ebenen und der uns umgebende
physikalische Raum, aber als mathematisches
Objekt ist er eine direkte Verallgemeinerung der Dinge, die wir hier
besprechen.
Die Menge aller reellen Zahlenpaare ist das kartesische Produkt der Menge
R mit sich selbst:
|  Zahlengerade  dreidimensionaler Raum (in Vorbereitung)  kartesisches Produkt | ||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||
|
Dieser Abschnitt kann von ''EinsteigerInnen'' ausgelassen werden.
Wir haben oben die Zeichenebene mit einem kartesischen Koordinatensystem
ausgestattet. Jeder Punkt ist durch ein Paar
Anstelle der kartesischen Koordinaten x und y kann die Position eines Punktes auch charakterisiert werden durch
Lediglich am Ursprung passiert ein kleines Malheur: Für ihn gilt
Diese Koordinaten heißen (ebene) Polarkoordinaten. Manche geometrischen Probleme lassen sich einfacher behandeln, wenn die Zeichenebene "durch die Brille der Polarkoordinaten" betrachtet wird. (Wenn Sie etwa für Ortsbestimmungen in der Arktis - von der Erdkrümmung einmal abgesehen - als Koordinaten den Abstand r vom Nordpol und die geographische Länge f verwenden, machen Sie nichts anderes). | Das Applet Ebene Polarkoordinaten veranschaulicht diese Definition. | ||||||||||||||||||||||||||||||||||||||||||||||
|
Jeder Punkt (ausgenommen der Ursprung) besitzt eindeutige Werte r und f der Polarkoordinaten. Daneben besitzt er auch eindeutige Werte x und y der kartesischen Koordinaten. Da sowohl im Paar |  Umrechnung kartesischer in Polarkoordinaten | ||||||||||||||||||||||||||||||||||||||||||||||
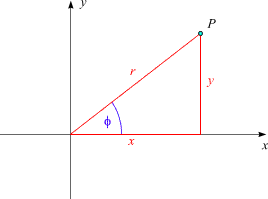 Spezialfälle für Werte von Polarkoordinaten sind:
| |||||||||||||||||||||||||||||||||||||||||||||||
|
Um ein Beispiel für ein weiteres Koordinatensystem anzuführen, erwähnen wir schiefwinkelige Koordinaten. Sie sind eine Verallgemeinerung der kartesischen Koordinaten und beruhen wie diese auf der Wahl zweier Achsen, die aber nun nicht aufeinander normal stehen müssen (und auf denen die Einheiten beliebig gewählt werden können). Während das Ablesen der kartesischen Koordinaten eines Punktes auf ein Rechteck führt (siehe oben), ist bei der Bestimmung schiefwinkeliger Koordinaten ein Parallelogramm zu verwenden, dessen Seiten parallel zu den Achsen sind: |  Parallelogramm (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||||||||||
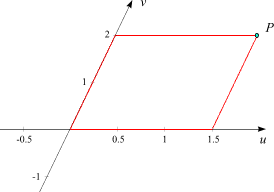 Die Koordinaten sind hier mit u und v bezeichnet. Der oben eingezeichnete Punkt P hat die Koordinaten | Applet Schiefwinkelige Koordinaten hilft, diese Definition besser zu verstehen. | ||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||
|
Dieser Abschnitt kann von ''EinsteigerInnen'' ausgelassen werden. Neben den hier besprochenen gibt es noch viele andere Koordinatensysteme. Der Sinn jedes Koordinatensystems ist es, die Position von Punkten durch Zahlen auszudrücken. Koordinatensysteme können ganz verschiedene Eigenschaften besitzen. So beruhen die kartesischen Koordinaten auf der Wahl zweier Achsen, wohingegen im Zusammenhang mit Polarkoordinaten weder von einer r-Achse noch von einer f-Achse die Rede war. Auch die Rolle des Ursprungs ist in beiden Systemen verschieden. Dennoch haben alle Kordinatensysteme etwas gemeinsam. Sie "überziehen" die Zeichenebene mit einem Muster aus Linien, den Koordinatenlinien. Eine Koordinatenlinie ist eine Linie (Kurve), entlang welcher sich der Wert einer der beiden Koordinaten nicht ändert. Wir wollen das aus diesen Linien gebildete Muster "Koordinaten-Raster" nennen. Es erinnert an die in einer Landkarte eingezeichneten Kurven, mit deren Hilfe die Längen- und Breitengrade eines Ortes abgelesen werden können. Ist in einer Skizze ein genügend feiner Raster dieser Linien eingezeichnet, so lassen sich die Koordinaten von Punkten bequem abzulesen. Nebenstehend finden Sie drei der Applets, auf die wir bereits oben verwiesen haben. Sie zeigen Ihnen die Koordinatenlinien dreier Koordinatensysteme auf Knopfdruck. Im Fall kartesischer (siehe oben) und schiefwinkeliger (siehe oben) Koordinaten sind alle Koordinatenlinien gerade. Der Koordinaten-Raster besteht aus zwei Scharen von zueinander parallelen Geraden. Diese Koordinaten werden daher geradlinig genannt. Sie besitzen Achsen (die jeweils selbst Koordinatenlinien sind, und zwar jene, entlang derer eine der beiden Koordinaten Null ist). Polarkoordinaten (siehe oben) sind ein Beispiel für krummlinige Koordinaten. Ihre Koordinatenlinien sind
| Kartesische Koordinaten Applet Schiefwinkelige Koordinaten Applet Ebene Polarkoordinaten | ||||||||||||||||||||||||||||||||||||||||||||||
|
Jedes Koordinatensystem hat seinen charakteristischen Raster und ermöglicht einen ganz bestimmten "Blick" auf die Zeichenebene und hat ein ganz besonderes "Flair". So manches Problem läßt sich leichter behandeln, wenn ein ihm angepasstes Koordinatensystem verwendet wird.
Der nebenstehende Button verbirgt eine Skizze,
die anhand eines Beispiels verdeutlicht, wie Koordinatenlinien
ganz allgemein aussehen können. Sie erinnern an ein deformiertes
Netz.
| |||||||||||||||||||||||||||||||||||||||||||||||
|
Die Koordinaten eines Punktes in Bezug auf ein Koordinatensystem
können in jene bezüglich eines anderen Koordinatensystems
umgerechnet werden.
Man spricht dann von einer
Koordinatentransformation. Insbesondere in der Physik spielt die gleichzeitige
Verwendung mehrerer (z. B. kartesischer, aber zueinander rotierter)
Koordinatensysteme
(oder Bezugssysteme, wie dort auch gesagt wird)
eine wichtige Rolle. |  Koordinaten- transformationen (in Vorbereitung) |
|
|
||
|
|
|
|
Zum Seitenanfang Zum Lexikon Zur Galerie Zum Kapitel Zeichenebene und Koordinatensystem der Galerie Zum Inhaltsverzeichnis der Mathematischen Hintergründe Zu den interaktiven Tests Zu den Mathe-Links und Online-Werkzeugen Zur Welcome Page |